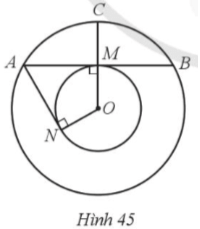
Cho hai đường tròn (O; R) và (O; 2R), Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R)

---

Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R). Gọi S1 là diện tích của hình tạo bởi cung ACB và dây AB của đường tròn (O; 2 R), S2 là diện tích của hình tạo bởi hai tiếp tuyến AM, AN và cung nhỏ MN của đường tròn (O; R) và S3 là diện tích của hình tròn (O; R) (Hình 45). Chứng minh S1 + S2 = S3.

Giải SBT Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên - Cánh diều

Bài 41 trang 121 SBT Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O; 2R). Một dây cung AB của đường tròn (O; 2R) tiếp xúc với đường tròn (O; R) tại M. Kẻ tiếp tuyến thứ hai AN của đường tròn (O; R). Gọi S1 là diện tích của hình tạo bởi cung ACB và dây AB của đường tròn (O; 2 R), S2 là diện tích của hình tạo bởi hai tiếp tuyến AM, AN và cung nhỏ MN của đường tròn (O; R) và S3 là diện tích của hình tròn (O; R) (Hình 45). Chứng minh S1 + S2 = S3.

Lời giải:

Do AM là tiếp tuyến của đường tròn (O; R) nên AM ⊥ OM tại M.

Xét tam giác OAM vuông tại M, theo định lí Pythagore, ta có:

OA² = OM² + AM²

Suy ra $AM=\sqrt{O{A}^2-O{M}^2}$ và $cos\widehat{AOM}=\frac{OM}{OA}=\frac{R}{2R}=\frac{1}{2}$

Do đó $AM=\sqrt{{\left(2R\right)}^2-R^2}=\sqrt{3R^2}=R\sqrt{3}$ và $\widehat{AOM}=60°.$

Xét ∆OAM (vuông tại M) và ∆OBM (vuông tại M) có:

OA = OB, cạnh OM chung

Do đó ∆OAM = ∆OBM (cạnh huyền – cạnh góc vuông).

Suy ra $AM=BM=\frac{AB}{2}$ và $\widehat{AOM}=\widehat{BOM}=\frac{\widehat{AOB}}{2}.$

Nên $AB=2AM=2R\sqrt{3}$ và $\widehat{AOB}=2\widehat{AOM}=2\cdot 60°=120°.$

Do AM, AN là hai tiếp tuyến của đường tròn (O; R) nên OA là tia phân giác của góc MON, suy ra $\widehat{MON}=2\widehat{AOM}=2\cdot 60°=120°.$

Ta có:

⦁ S₁ = Diện tích hình quạt tròn AOB ‒ Diện tích tam giác OAB

Suy ra $S_1=\frac{\pi {\left(2R\right)}^2\cdot 120}{360}-\frac{1}{2}\cdot R\cdot 2R\sqrt{3}=R^2\left(\frac{4\pi }{3}-\sqrt{3}\right);$

⦁ S₂ = 2. Diện tích tam giác OAM ‒ Diện tích hình quạt tròn MON

Suy ra $S_2=2\cdot \frac{1}{2}\cdot R\cdot R\sqrt{3}-\frac{\pi R\cdot 120}{360}=R^2\left(\sqrt{3}-\frac{\pi }{3}\right);$

⦁ S₃ = Diện tích hình tròn (O; R) = πR².

Khi đó $S_1+S_2=R^2\left(\frac{4\pi }{3}-\sqrt{3}\right)+R^2\left(\sqrt{3}-\frac{\pi }{3}\right)$

                       $=R^2\left(\frac{4\pi }{3}-\sqrt{3}+\sqrt{3}-\frac{\pi }{3}\right)=\pi R^2=S_3.$

Vậy S₁ + S₂ = S₃.

Lời giải SBT Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên hay khác:

• Bài 37 trang 120 SBT Toán 9 Tập 1: Hoàn thành số liệu ở bảng sau (làm tròn kết quả đến hàng phần trăm của đơn vị đo đã cho nếu cần, lấy π ≈ 3,14): ....

• Bài 38 trang 120 SBT Toán 9 Tập 1: Chuyển động của Mặt Trăng quanh Trái Đất theo một quỹ đạo là gần giống đường tròn với tốc độ không đổi. Giả thiết quỹ đạo này là đường tròn ....

• Bài 39 trang 121 SBT Toán 9 Tập 1: Cho hình thoi ABCD có cạnh AB = 5 cm, đường chéo AC = 8 cm. Vẽ các đường tròn (A; 5 cm), (C; 3 cm). Đường tròn (C) cắt BC, CD lần lượt tại E, F ....

• Bài 40 trang 121 SBT Toán 9 Tập 1: Cho tam giác ABE vuông cân tại A với AB = AE = 2a. Vẽ đường tròn tâm O đường kính AB và đường tròn tâm O’ đường kính AE. Gọi M là giao điểm khác A ....

• Bài 42 trang 121 SBT Toán 9 Tập 1: Hai ròng rọc có dạng hình tròn (O; 4a) và (O’; a) với hai tiếp tuyến chung MN và PQ cắt nhau tại A ....

• Bài 43 trang 122 SBT Toán 9 Tập 1: Cho hình chữ nhật ABCD với AB = 10 cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q ....

• Bài 44 trang 122 SBT Toán 9 Tập 1: Bác Long dự định mua gỗ để làm một mặt bàn. Mặt bàn có dạng ở giữa là hình chữ nhật với chiều rộng 1,2 m, chiều dài 1,8 m ....

• Bài 45 trang 122 SBT Toán 9 Tập 1: Hình 49 mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn (O; 15 cm), (O; 10 cm) ....

• Bài 46 trang 122 SBT Toán 9 Tập 1: Cho đường tròn tâm O bán kính OM = 8 cm. Gọi O’ là trung điểm của đoạn thẳng OM, vẽ đường tròn tâm O’ bán kính 16 cm. Trong đường tròn (O), kẻ dây AB đi qua O’ ....