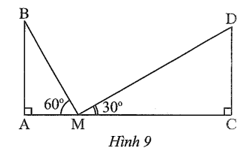
Hai trụ điện cùng chiều cao được dựng thẳng đứng ở hai bên lề đối diện một đại lộ rộng 80 m (AC = 80 m)
Hai trụ điện cùng chiều cao được dựng thẳng đứng ở hai bên lề đối diện một đại lộ rộng 80 m (AC = 80 m). Từ một điểm M trên mặt đường giữa hai trụ người ta nhìn thấy đỉnh hai trụ điện với các góc nâng lần lượt là 60° và 30°. Tính chiều cao của trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện.
Giải sách bài tập Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn - Chân trời sáng tạo
Bài 8 trang 69 sách bài tập Toán 9 Tập 1: Hai trụ điện cùng chiều cao được dựng thẳng đứng ở hai bên lề đối diện một đại lộ rộng 80 m (AC = 80 m). Từ một điểm M trên mặt đường giữa hai trụ người ta nhìn thấy đỉnh hai trụ điện với các góc nâng lần lượt là 60° và 30°. Tính chiều cao của trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện.
Lời giải:
Xét ∆ABM vuông tại A, ta có: cot^AMB=AMAB.
Suy ra AM=AB⋅cot^AMB=AB⋅cot60°
Xét ∆CMD vuông tại C, ta có:
Suy ra
Mà AB = CD nên
Ta có: AC = AM + CM
Suy ra:
Hay
Do đó
Như vậy, chiều cao của trụ điện là mét.
Khoảng cách từ điểm M đến trụ điện AB là:
Khoảng cách từ điểm M đến trụ điện CD là:
MC = AC ‒ AM = 80 ‒ 20 = 60 (m).
Lời giải SBT Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn hay khác: