Vẽ hình và chứng minh phần b của Ví dụ 2. Cho đường tròn (O) và dây AB không là đường kính của (O)
Vẽ hình và chứng minh phần b của
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 17: Vị trí tương đối của hai đường tròn - Kết nối tri thức
Bài 5.23 trang 68 sách bài tập Toán 9 Tập 1: Vẽ hình và chứng minh phần b của Ví dụ 2.
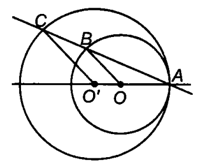
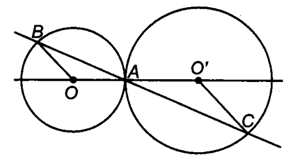
Cho đường tròn (O) và dây AB không là đường kính của (O). Vị trí tương đối của (O) và (O'; O'C) sẽ như thế nào nếu O' thẳng hàng với O và A, nhưng nằm ngoài đoạn OA?
Lời giải:
TH1: OO' nằm cùng phía đối với A:
Do O'C // OB nên ∆OAB ᔕ ∆O'AC (g.g).
Mà OAB cân tại O nên O'AC cân tại O', suy ra O'A = O'C.
Do đó ta có OO' = O'A – OA = O'C – OA, suy ra (O'; O'C) tiếp xúc trong với (O; OA). (đpcm)
TH2: OO' nằm khác phía đối với A:
Do O'C // OB nên ∆OAB ᔕ ∆O'AC (g.g).
Mà OAB cân tại O nên O'AC cân tại O', suy ra O'A = O'C.
Suy ra OO' = O'A + OA = O'C + OA.
Do đó (O'; O'C) tiếp xúc ngoài với (O; OA). (đpcm)
Lời giải SBT Toán 9 Bài 17: Vị trí tương đối của hai đường tròn hay khác: