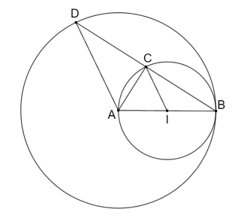
Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB)
Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB).
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 17: Vị trí tương đối của hai đường tròn - Kết nối tri thức
Bài 5.25 trang 68 sách bài tập Toán 9 Tập 1: Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB).
a) Hai đường tròn (I) và (A) nói trên có vị trí tương đối như thế nào?
b) Đường thẳng đi qua B, cắt các đường tròn (I) và (A) làn lượt tại C và D. Hãy so sánh các độ dài BC và CD.
Lời giải:
a) Vì I là trung điểm AB nên ta có AI = AB – IB.
Do đó hai đường tròn (I; IB) và (A; AB) tiếp xúc trong với nhau.
b) Vì D nằm trên đường tròn (A; AB) nên AD = AB, suy ra tam giác ACB cân tại A.
Xét tam giác ACB có:
CI là trung tuyến của tam giác (I là trung điểm AB)
(CI là bán kính của (I), AB là đường kính của (I))
Suy ra tam giác ACB vuông tại C, do đó AC ⊥ CB hay AC ⊥ BD.
Tam giác ABD cân tại A có AC là đường cao nên AC đồng thời là đường trung tuyến của tam giác ABD, suy ra C là trung điểm BD hay CB = CD.
Vậy CB = CD.
Lời giải SBT Toán 9 Bài 17: Vị trí tương đối của hai đường tròn hay khác: