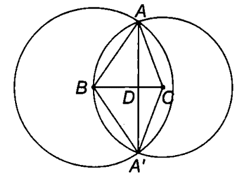
Cho tam giác ABC. Chứng minh rằng hai đường tròn (B; BA) và (C; CA) cắt nhau. Gọi A' là giao điểm khác A của hai đường tròn đó

Cho tam giác ABC.

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 17: Vị trí tương đối của hai đường tròn - Kết nối tri thức

Bài 5.26 trang 68 sách bài tập Toán 9 Tập 1: Cho tam giác ABC.

a) Chứng minh rằng hai đường tròn (B; BA) và (C; CA) cắt nhau. Gọi A' là giao điểm khác A của hai đường tròn đó.

b) Chứng minh rằng A và A' đối xứng nhau qua BC.

c) Biết rằng AA' = 24 cm, AB = 15 cm và AC = 13 cm. Tính độ dài BC.

Lời giải:

Cho tam giác ABC. Chứng minh rằng hai đường tròn (B; BA) và (C; CA) cắt nhau. Gọi A' là giao điểm khác A của hai đường tròn đó

a) Áp dụng bất đẳng thức tam giác với tam giác ABC, ta có:

AB + AC > BC > AB – AC

Do đó tam giác (B; BA) và (C; CA) cắt nhau. (đpcm)

b) Xét ∆ABC và ∆A'BC có:

AB = A'B (A và A' cùng nằm trên đường tròn (B))

AC = A'C (A và A' cùng nằm trên đường tròn (C))

Chung cạnh BC

Do đó ∆ABC = ∆A'BC (c.c.c).

Suy ra $\hat{A B C} = \hat{A' B C}$ (hai góc tương ứng) hay BC là đường phân giác của $\hat{A B A'} .$

Mà tam giác ABA' cân tại B do AB = A'B, suy ra BC là đường phân giác của góc $\hat{A B A'} .$ cũng đồng thời là đường trung trực của AA'.

Do đó A và A' đối xứng với nhau qua BC. (đpcm)

c) Gọi D là giao điểm của BC và AA'.

Theo câu b) ta có AD = DA' (do A và A' đối xứng qua BC) và BC ⊥ AA', suy ra tam giác ABD và ACD vuông tại D.

Do AD = A'D nên $A D = A' D = \frac{A A'}{2} = \frac{24}{2} = 12$ (cm).

+ Áp dụng định lý Pythagore với tam giác ABD, ta có:

$B D = \sqrt{A B^{2} - A D^{2}} = \sqrt{15^{2} - 12^{2}} = 9$ (cm)

+ Áp dụng định lý Pythagore với tam giác ADC ta có:

$D C = \sqrt{A C^{2} - A D^{2}} = \sqrt{13^{2} - 12^{2}} = 5$ (cm).

Vậy BC = BD + CD = 9 + 5 = 14 (cm).

Lời giải SBT Toán 9 Bài 17: Vị trí tương đối của hai đường tròn hay khác:

SBT Toán 9 Kết nối tri thức