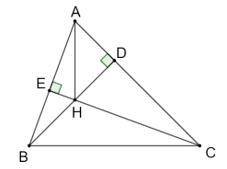
Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng
Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng:
Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 14: Cung và dây của một đường tròn - Kết nối tri thức
Bài 5.6 trang 59 sách bài tập Toán 9 Tập 1: Cho tam giác nhọn ABC, hai đường cao BD và CE cắt nhau tại H. Chứng minh rằng:
a) Bốn điểm A, E, H, D cùng thuộc một đường tròn.
b) AH > DE.
Lời giải:
a) Tam giác AEH vuông tại E nên 3 điểm A, E, H cùng nằm trên đường tròn đường kính AH.
Tam giác ADH vuông tại D nên 3 điểm A, D, H cùng nằm trên đường tròn đường kính AH.
Vậy 4 điểm A, E, H, D cùng nằm trên đường tròn đường kính AH.
b) Do góc A là góc nhọn nên dây DE của đường tròn đường kính AH không đi qua tâm của đường tròn (không phải đường kính).
Mà AH là đường kính của đường tròn đang xét nên AH < DE. (đpcm)
Lời giải SBT Toán 9 Bài 14: Cung và dây của một đường tròn hay khác: