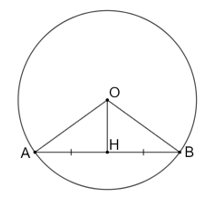
Gọi H là trung điểm của dây AB không đi qua tâm của đường tròn (O). Chứng minh rằng OH ⊥ AB

Gọi H là trung điểm của dây AB không đi qua tâm của đường tròn (O).

Haylamdo biên soạn và sưu tầm lời giải sách bài tập Toán 9 Bài 14: Cung và dây của một đường tròn - Kết nối tri thức

Bài 5.8 trang 59 sách bài tập Toán 9 Tập 1: Gọi H là trung điểm của dây AB không đi qua tâm của đường tròn (O).

a) Chứng minh rằng OH ⊥ AB.

b) Tính khoảng cách từ O đến AB, biết rằng AB = 8 cm và bán kính của (O) bằng 5 cm.

Lời giải:

Gọi H là trung điểm của dây AB không đi qua tâm của đường tròn (O). Chứng minh rằng OH ⊥ AB

a) Vì OA = OB (bán kính đường tròn (O)) nên ∆OAB cân tại O.

H là trung điểm của AB nên OH là đường trung tuyến đồng thời là đường cao của tam giác cân OAB.

Vây OH ⊥ AB. (đpcm)

b) H là trung điểm của AB nên $A H = \frac{A B}{2} = \frac{8}{2} = 4$ (cm).

Áp dụng định lý Pythagore với tam giác OAH ta có:

$O H = \sqrt{O A^{2} - A H^{2}} = \sqrt{5^{2} - 4^{2}} = 3$ (cm).

Vậy khoảng cách từ O đến AB là 3 cm.

Lời giải SBT Toán 9 Bài 14: Cung và dây của một đường tròn hay khác:

SBT Toán 9 Kết nối tri thức