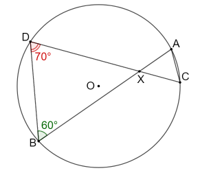
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại X. Tính số đo các góc của tam giác AXC

Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại X. Tính số đo các góc của tam giác AXC, biết rằng

Giải sách bài tập Toán 9 Bài 27: Góc nội tiếp - Kết nối tri thức

Bài 9.4 trang 51 sách bài tập Toán 9 Tập 2: Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại X. Tính số đo các góc của tam giác AXC, biết rằng $\widehat{XBD}=60°,\widehat{XDB}=70°.$

Lời giải:

Xét trong đường tròn (O), ta có:

Hai góc nội tiếp ACX và XBD cùng chắn cung nhỏ $\stackrel{⏜}{AD}$ nên $\widehat{ACX}=\widehat{XBD}=60°$

Hai góc nội tiếp CAX và XDB cùng chắn cung nhỏ $\stackrel{⏜}{CB}$ nên

$\widehat{CAX}=\widehat{XDB}=70°$

Tổng các góc trong tam giác ACX bằng 180° nên

$\widehat{AXC}=180°-\widehat{ACX}-\widehat{CAX}=180°-60°-70°=50°$

Vậy $\widehat{ACX}=60°, \widehat{CAX}=70° và \widehat{AXC}=50°$

Lời giải SBT Toán 9 Bài 27: Góc nội tiếp hay khác:

• Bài 9.1 trang 50 sách bài tập Toán 9 Tập 2: Hình nào dưới đây vẽ một góc nội tiếp của đường tròn? ...

• Bài 9.2 trang 50 sách bài tập Toán 9 Tập 2: Cho điểm A nằm trên cung lớn BC của đường tròn (O) và kí hiệu $\stackrel{⏜}{BC}$ là cung nhỏ BC. Vẽ bảng sau vào vở và viết số đo còn lại của góc hoặc cung tương ứng vào ô trống trong mỗi trường hợp ...

• Bài 9.3 trang 50 sách bài tập Toán 9 Tập 2: Cho AB và CD là hai đường kính của đường tròn (O). Biết rằng $\widehat{AOC}$ = 80°, tính số đo của các góc ABC, ADC và ABD. ...

• Bài 9.5 trang 51 sách bài tập Toán 9 Tập 2: Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn $\stackrel{⏜}{BC}$. Biết rằng $\widehat{OBA}=30°,\widehat{OCA}=40°.$ Tính số đo các góc của tam giác ABC. ...

• Bài 9.6 trang 51 sách bài tập Toán 9 Tập 2: Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn sao cho C khác A, B. Lấy E là điểm đối xứng của A qua C. Chứng minh rằng BE = BA. ...

• Bài 9.7 trang 51 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC cân tại A. Đường tròn đường kính AB cắt các cạnh AC, BC của tam giác ABC tại X và Y (X khác A, Y khác B). ...