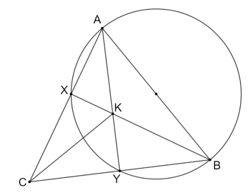
Cho tam giác nhọn ABC cân tại A. Đường tròn đường kính AB cắt các cạnh AC, BC của tam giác ABC tại X và Y
Cho tam giác nhọn ABC cân tại A. Đường tròn đường kính AB cắt các cạnh AC, BC của tam giác ABC tại X và Y (X khác A, Y khác B).
Giải sách bài tập Toán 9 Bài 27: Góc nội tiếp - Kết nối tri thức
Bài 9.7 trang 51 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC cân tại A. Đường tròn đường kính AB cắt các cạnh AC, BC của tam giác ABC tại X và Y (X khác A, Y khác B).
a) Chứng minh rằng tam giác CXYcân tại Y.
b) Cho BX cắt AY tại K. Chứng minh rằng CK vuông góc với AB.
Lời giải:
a) Do các góc AXB và AYB là các góc nội tiếp đường tròn đường kính AB và chắn nửa đường tròn nên hay AY ⊥ BC và BX ⊥ AC.
Vì tam giác ABC cân tại A nên đường cao AY đồng thời là đường trung tuyến của tam giác.
Do đó Y là trung điểm của BC, suy ra Y là tâm đường tròn ngoại tiếp tam giác BXC vuông tại X.
Vì vậy YC = YX hay tam giác CXY cân tại Y (đpcm).
b) Vì AX, BY là các đường cao của tam giác ABC nên K là trực tâm của tam giác ABC.
Do đó CK ⊥ AB (đpcm).
Lời giải SBT Toán 9 Bài 27: Góc nội tiếp hay khác: