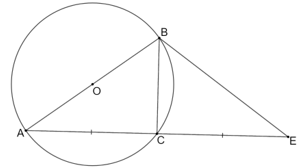
Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn sao cho C khác A, B

Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn sao cho C khác A, B. Lấy E là điểm đối xứng của A qua C. Chứng minh rằng BE = BA.

Giải sách bài tập Toán 9 Bài 27: Góc nội tiếp - Kết nối tri thức

Bài 9.6 trang 51 sách bài tập Toán 9 Tập 2: Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn sao cho C khác A, B. Lấy E là điểm đối xứng của A qua C. Chứng minh rằng BE = BA.

Lời giải:

Vì ABC là góc nội tiếp của đường tròn (O) chắn nửa đường tròn nên $\widehat{ACB}=90°$ hay BC ⊥ AE.

E đối xứng với A qua C nên CA = CE.

Xét ∆BCA và ∆BCE có:

Chung cạnh BC

$\widehat{BCA}=\widehat{BCE}=90°$ (vì BC ⊥ AE)

CA = CE

Suy ra ∆BCA = ∆BCE (c.g.c), do đó BA = BE (đpcm).

Lời giải SBT Toán 9 Bài 27: Góc nội tiếp hay khác:

• Bài 9.1 trang 50 sách bài tập Toán 9 Tập 2: Hình nào dưới đây vẽ một góc nội tiếp của đường tròn? ...

• Bài 9.2 trang 50 sách bài tập Toán 9 Tập 2: Cho điểm A nằm trên cung lớn BC của đường tròn (O) và kí hiệu $\stackrel{⏜}{BC}$ là cung nhỏ BC. Vẽ bảng sau vào vở và viết số đo còn lại của góc hoặc cung tương ứng vào ô trống trong mỗi trường hợp ...

• Bài 9.3 trang 50 sách bài tập Toán 9 Tập 2: Cho AB và CD là hai đường kính của đường tròn (O). Biết rằng $\widehat{AOC}$ = 80°, tính số đo của các góc ABC, ADC và ABD. ...

• Bài 9.4 trang 51 sách bài tập Toán 9 Tập 2: Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại X. Tính số đo các góc của tam giác AXC, biết rằng $\widehat{XBD}=60°,\widehat{XDB}=70°.$ ...

• Bài 9.5 trang 51 sách bài tập Toán 9 Tập 2: Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn $\stackrel{⏜}{BC}$. Biết rằng $\widehat{OBA}=30°,\widehat{OCA}=40°.$ Tính số đo các góc của tam giác ABC. ...

• Bài 9.7 trang 51 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC cân tại A. Đường tròn đường kính AB cắt các cạnh AC, BC của tam giác ABC tại X và Y (X khác A, Y khác B). ...