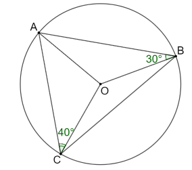
Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn góc BC

Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn . Biết rằng Tính số đo các góc của tam giác ABC.

Giải sách bài tập Toán 9 Bài 27: Góc nội tiếp - Kết nối tri thức

Bài 9.5 trang 51 sách bài tập Toán 9 Tập 2: Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn $\stackrel{⏜}{BC}$. Biết rằng $\widehat{OBA}=30°,\widehat{OCA}=40°.$Tính số đo các góc của tam giác ABC.

Lời giải:

Vì OA = OB nên tam giác OAB cân tại O, do đó

$\widehat{AOB}=180°-2\widehat{OBA}=180°-2.30°=120°$

Vì OA = OC nên tam giác OAC cân tại O, do đó

$\widehat{AOC}=180°-2\widehat{OCA}=180°-2.40°=100°$

Xét trong đường tròn (O), ta có:

Góc nội tiếp ABC và góc ở tâm AOC cùng chắn cung nhỏ $\stackrel{⏜}{AC}$ nên $\widehat{ABC}=\frac{1}{2}\widehat{AOC}=\frac{100°}{2}=50°$

Góc nội tiếp ACB và góc ở tâm AOB cùng chắn cung nhỏ $\stackrel{⏜}{AB}$ nên $\widehat{ACB}=\frac{1}{2}\widehat{AOB}=\frac{120°}{2}=60°$

Tổng các góc trong tam giác ABC bằng 180° nên

$\widehat{BAC}=180°-\widehat{ABC}-\widehat{ACB}=180°-50°-60°=70°$

Vậy $\widehat{ABC}=50°, \widehat{ACB}=60°, \widehat{BAC}=70°$ 

Lời giải SBT Toán 9 Bài 27: Góc nội tiếp hay khác:

• Bài 9.1 trang 50 sách bài tập Toán 9 Tập 2: Hình nào dưới đây vẽ một góc nội tiếp của đường tròn? ...

• Bài 9.2 trang 50 sách bài tập Toán 9 Tập 2: Cho điểm A nằm trên cung lớn BC của đường tròn (O) và kí hiệu $\stackrel{⏜}{BC}$ là cung nhỏ BC. Vẽ bảng sau vào vở và viết số đo còn lại của góc hoặc cung tương ứng vào ô trống trong mỗi trường hợp ...

• Bài 9.3 trang 50 sách bài tập Toán 9 Tập 2: Cho AB và CD là hai đường kính của đường tròn (O). Biết rằng $\widehat{AOC}$ = 80°, tính số đo của các góc ABC, ADC và ABD. ...

• Bài 9.4 trang 51 sách bài tập Toán 9 Tập 2: Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại X. Tính số đo các góc của tam giác AXC, biết rằng $\widehat{XBD}=60°,\widehat{XDB}=70°.$ ...

• Bài 9.6 trang 51 sách bài tập Toán 9 Tập 2: Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn sao cho C khác A, B. Lấy E là điểm đối xứng của A qua C. Chứng minh rằng BE = BA. ...

• Bài 9.7 trang 51 sách bài tập Toán 9 Tập 2: Cho tam giác nhọn ABC cân tại A. Đường tròn đường kính AB cắt các cạnh AC, BC của tam giác ABC tại X và Y (X khác A, Y khác B). ...