Lý thuyết Tin học 7 Chân trời sáng tạo Bài 13: Thuật toán tìm kiếm
Haylamdo biên soạn và sưu tầm tóm tắt lý thuyết Tin học lớp 7 Bài 13: Thuật toán tìm kiếm sách Chân trời sáng tạo hay nhất, ngắn gọn sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Tin học 7.
Lý thuyết Tin học 7 Chân trời sáng tạo Bài 13: Thuật toán tìm kiếm
Chỉ từ 100k mua trọn bộ lý thuyết Tin 7 Chân trời sáng tạo (cả năm) bản word trình bày đẹp mắt, dễ dàng chỉnh sửa:
- B1: gửi phí vào tk:
0711000255837- NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
1. Thuật toán tìm kiếm tuần tự
- Thuật toán tìm kiếm tuần tự thực hiện so sánh lần lượt phần tử đầu tiên của dãy với giá trị cần tìm, việc tìm kiếm kết thúc khi tìm thấy hoặc đã duyệt hết các phần tử trong dãy.
Ví dụ: Có 9 thẻ số, mỗi thẻ được ghi số ở một mặt và mặt còn lại không ghi gì. Đặt úp các thẻ số trên mặt bàn và xếp thành một dãy. Tìm một số bất kì trong dãy.
Hình 1. Các thẻ được ghi số ở mặt úp.
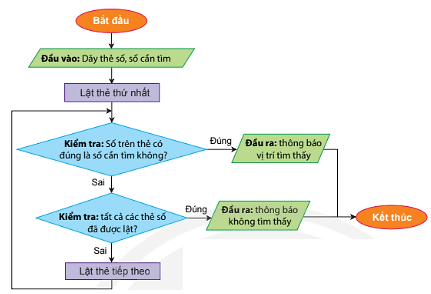
Hướng dẫn: Thuật toán thực hiện lặp đi lặp lại việc duyệt từng thẻ số, vòng lặp sẽ kết thúc khi tìm thấy số cần tìm hoặc đã duyệt hết các thẻ số.
Hình 2. Sơ đồ khối mô tả thuật toán tìm kiếm tuần tự để tìm một số trong dãy thẻ số.
2. Thuật toán tìm kiếm nhị phân
- Thuật toán tìm kiếm nhị phân thực hiện chia bài toán tìm kiếm ban đầu thành những bài toán tìm kiếm nhỏ hơn.
Ví dụ: Có 9 thẻ số, mỗi thẻ được ghi số ở một mặt và mặt còn lại không ghi gì. Đặt úp các thẻ số trên mặt bàn và xếp thành một dãy. Tìm một số bất kì trong dãy.
Hình 3. Các thẻ được ghi số ở mặt úp.
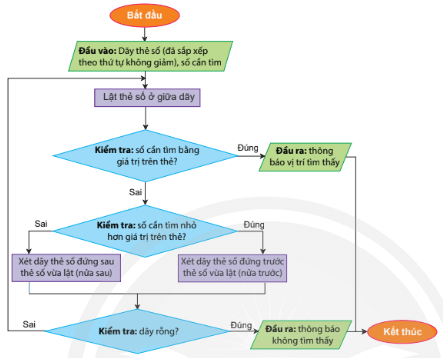
Hướng dẫn:
Hình 4. Sơ đồ khối mô tả thuật toán tìm kiếm nhị phân để tìm một số trong dãy thẻ số.
Lưu ý:
- Thẻ số ở giữa dãy có số thứ tự là phần nguyên của phép chia:
(Số lượng thẻ của dãy +1) : 2.
- Khi dãy chỉ còn một thẻ số thì nửa trước (hoặc nửa sau) là dãy rỗng.
⇒ Kết luận
- Thuật toán tìm kiếm nhị phân áp dụng với dãy giá trị đã được sắp xếp. Ở mỗi lần lặp thực hiện:
+ Bước 1. So sánh giá trị cần tìm với giá trị của phần tử giữa dãy đang xét.
+ Bước 2. Nếu bằng nhau thì thông báo vị trí tìm thấy và kết thúc.
+ Bước 3. Nếu nhỏ hơn thì xét dãy ở nửa trước, nếu lớn hơn thì xét ở dãy nửa sau.
+ Bước 4. Nếu dãy rỗng thì thông báo không tìm thấy và kết thúc tìm kiếm, không thì quay lại Bước 1.
- Sắp xếp và tìm kiếm: Sắp xếp giúp việc tìm kiếm được thực hiện nhanh hơn, hiệu quả hơn.