Cho tam giác OAB vuông cân tại O cạnh OA = a. Khẳng định nào sau đây sai:

Cho tam giác OAB vuông cân tại O cạnh OA = a. Khẳng định nào sau đây sai:

Đáp án đúng là: C

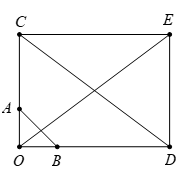
Dựa vào các đáp án, ta có nhận xét sau:

- Gọi C nằm trên tia đối của tia AO sao cho

$OC=3OA$ $\Rightarrow 3\overrightarrow{OA}=\overrightarrow{OC}.$

Và D nằm trên tia đối của tia BO sao cho

$OD=4OB$ $\Rightarrow 4\overrightarrow{OB}=\overrightarrow{OD}.$

Dựng hình chữ nhật OCED suy ra $\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{OE}$ (quy tắc hình bình hành).

Ta có: $\left|3\overrightarrow{OA}+4\overrightarrow{OB}\right|=\left|\overrightarrow{OC}+\overrightarrow{OD}\right|=\left|\overrightarrow{OE}\right|=OE=CD=\sqrt{O{C}^2+O{D}^2}=5a.$ 

Do đó, A đúng

- B đúng, vì $\left|2\overrightarrow{OA}\right|+\left|3\overrightarrow{OB}\right|=2\left|\overrightarrow{OA}\right|+3\left|\overrightarrow{OB}\right|=2a+3a=5a.$

- D đúng, vì $\left|11\overrightarrow{OA}\right|-\left|6\overrightarrow{OB}\right|=11\left|\overrightarrow{OA}\right|-6\left|\overrightarrow{OB}\right|=11a-6a=5a.$

Vậy chỉ còn đáp án C.