Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.

Câu hỏi:

A. $\overrightarrow{MN}=\overrightarrow{QP};$

B. $\left|\overrightarrow{QP}\right|=\left|\overrightarrow{MN}\right|;$

C. $\overrightarrow{MQ}=\overrightarrow{NP};$

D. $\left|\overrightarrow{MN}\right|=\left|\overrightarrow{AC}\right|.$

Trả lời:

Đáp án đúng là: D

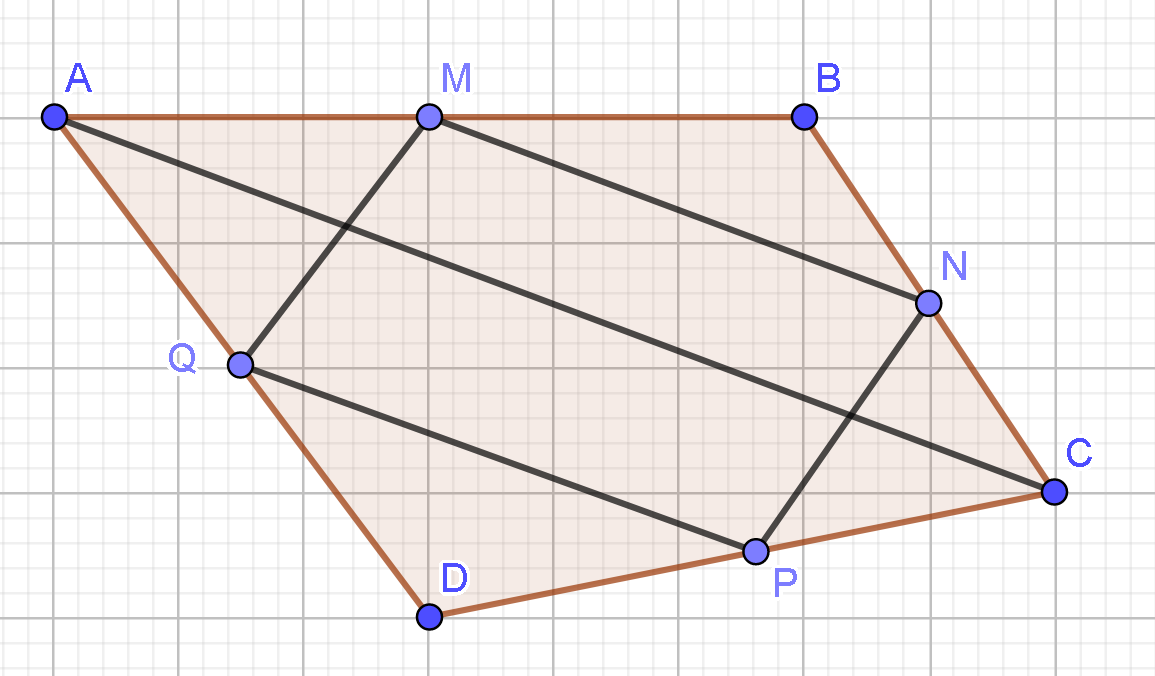
Ta có: $\left\{\begin{array}{l}MN\parallel PQ\\ MN=PQ\end{array}\right.$ (do cùng song song và bằng $\frac{1}{2}AC$).  

Do đó MNPQ là hình bình hành.

Vì MNPQ là hình bình hành nên $\overrightarrow{MN}=\overrightarrow{QP};$ $\left|\overrightarrow{QP}\right|=\left|\overrightarrow{MN}\right|;$ $\overrightarrow{MQ}=\overrightarrow{NP}.$