Có thể lập được bao nhiêu số có hai chữ số từ các số 1; 2; 3; 4 sao cho hai chữ số của số lập được đều khác nhau A. 4; B. 16; C. 12; D. 10.
Câu hỏi:
Có thể lập được bao nhiêu số có hai chữ số từ các số 1; 2; 3; 4 sao cho hai chữ số của số lập được đều khác nhau
A. 4;
B. 16;
C. 12;
D. 10.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Có 4 cách chọn chữ số hàng chục, có ba cách chọn chữ số hàng đơn vị (khác với chữ số hàng chục đã chọn).
Chọn chữ số hàng chục và chọn chữ số hàng đơn vị là hai hành động được diễn ra liên tiếp nên ta dùng quy tắc nhân.
Số các số lập được là: 4 . 3 = 12 (số)
Xem thêm bài tập Toán 10 Cánh diều có lời giải hay khác:
Câu 1:
Một lớp có 31 học sinh nam và 16 học sinh nữ. Có bao nhiêu cách chọn một học sinh làm lớp trưởng của lớp.
Xem lời giải »
Câu 2:
Bạn An dự định mua quà sinh nhật cho mẹ là một dây chuyền. Có ba kiểu mặt dây chuyền là: hình cỏ bốn lá, hình trái tim và hình giọt nước; có 2 loại dây là dạng xoắn, dạng chỉ. Hỏi bạn An có mấy cách chọn dây chuyền tặng mẹ.
Xem lời giải »
Câu 3:
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
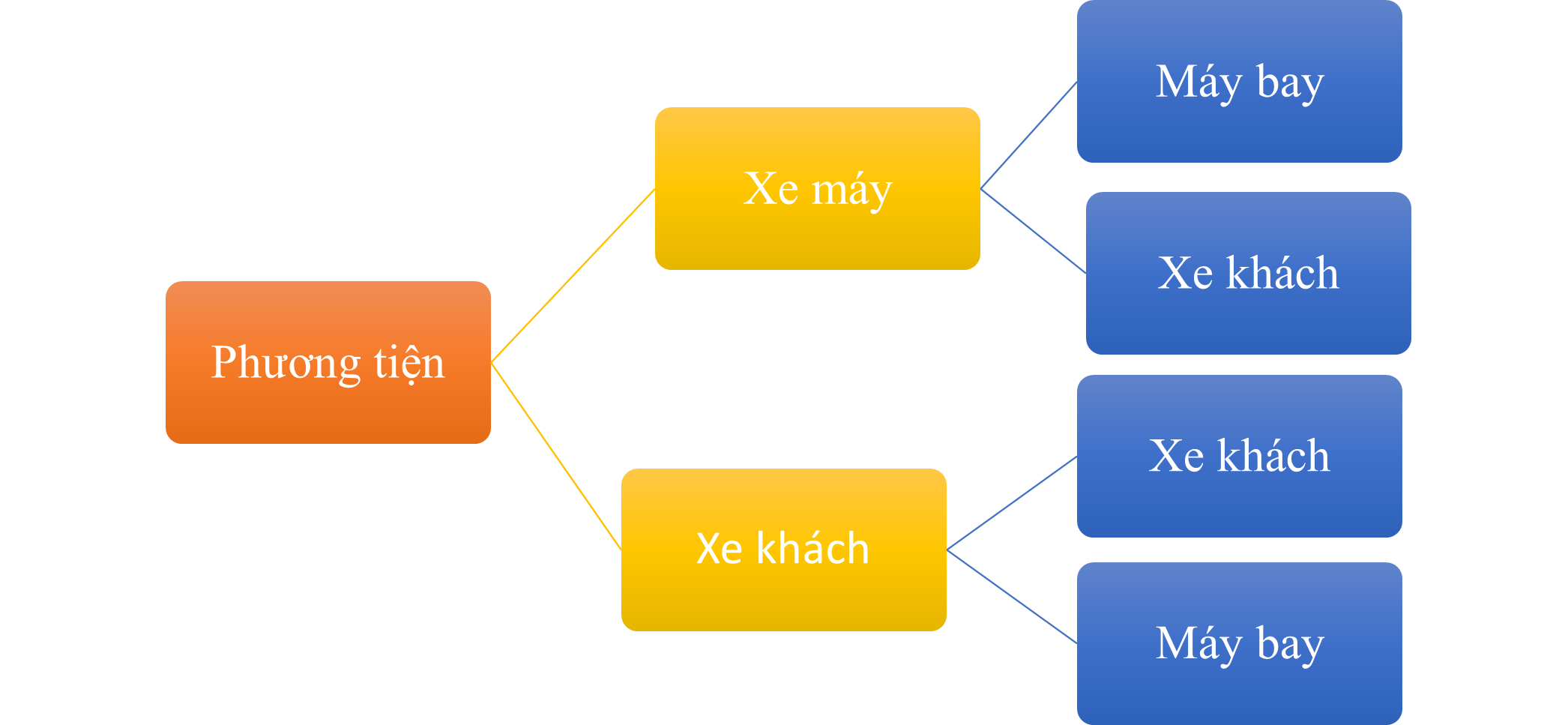
Hỏi bạn Khoa có mấy cách chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt.
Xem lời giải »
Câu 4:
Từ các chữ số 6; 7; 8; 9, có thể lập được bao nhiêu chữ số tự nhiên có 3 chữ số.
Xem lời giải »
Câu 5:
Hà dự định mua một cây bút và một quyển vở làm quà sinh nhật. Các cây bút có 6 màu vỏ khác nhau và các quyển vở có 5 màu bìa khác nhau. Hỏi bạn Hà có bao nhiêu cách chọn quà sinh nhật.
Xem lời giải »


