Giải Toán 10 trang 12 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm giải Toán 10 trang 12 Tập 2 trong Bài 2: Giải bất phương trình bậc hai một ẩn Toán lớp 10 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 12.

Giải Toán 10 trang 12 Tập 2 Chân trời sáng tạo

Thực hành 2 trang 12 Toán lớp 10 Tập 2: Giải các bất phương trình bậc hai sau:

a) 15x² + 7x – 2 ≤ 0;

b) – 2x² + x – 3 < 0.

Lời giải:

a) Xét tam thức bậc hai f(x) = 15x² + 7x – 2 có ∆ = 7² – 4.(-2).15 = 169 > 0. Do đó f(x) có hai nghiệm phân biệt x₁ = $\frac{1}{5}$ , x₂ = $-\frac{2}{3}$ và a = 15 > 0.

Suy ra f(x) nhỏ hơn hoặc bằng 0 khi x thuộc khoảng .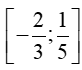

Vậy bất phương trình 15x² + 7x – 2 ≤ 0 có tập nghiệm là S = .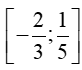

b) Xét tam thức bậc hai g(x) = – 2x² + x – 3 có ∆ = 1² – 4.(-2).(-3) = -23 < 0 và a = -2. Do đó g(x) vô nghiệm.

Suy ra g(x) luôn âm với mọi x ∈ ℝ.

Vậy bất phương trình – 2x² + x – 3 < 0 có tập nghiệm S = ℝ.

Vận dụng trang 12 Toán lớp 10 Tập 2: Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng đó có lãi.

Lời giải:

Ta có x là giá bán của một kilôgam gạo

Xét tam thức bậc hai f(x) = - 3x² + 200x – 2 325 có ∆ = 200² – 4.(-3).(-2 325) = 12 100 > 0. Do đó phương trình có hai nghiệm phân biệt là x₁ = 15 và x₂ = $\frac{155}{3}$ và a = -3 < 0.

Suy ra f(x) dương khi x thuộc khoảng $\left(15;\frac{155}{3}\right)$ .

Cửa hàng có lãi từ loại gạo đó khi I > 0 hay f(x) > 0.

Suy ra với x thuộc khoảng $\left(15;\frac{155}{3}\right)$ thì cửa hàng có lãi từ loại gạo đó.

Vậy với giá bán gạo trong khoảng 15 nghìn đồng đến $\frac{155}{3}$ nghìn đồng thì cửa hàng có lãi từ loại gạo đó.

Bài 1 trang 12 Toán lớp 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:

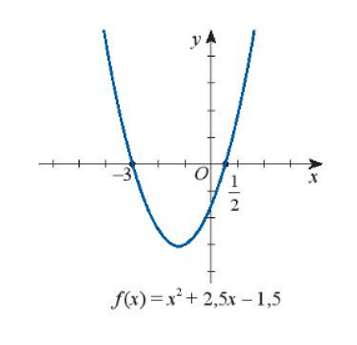
a) x² + 2,5x – 1,5 ≤ 0;

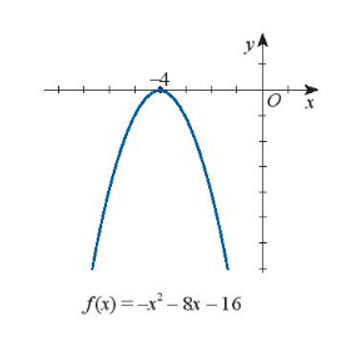
b) – x² – 8x – 16 < 0

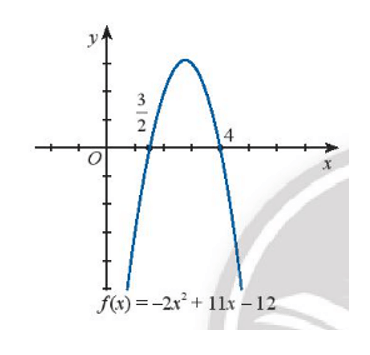
c) – 2x² + 11x – 12 > 0

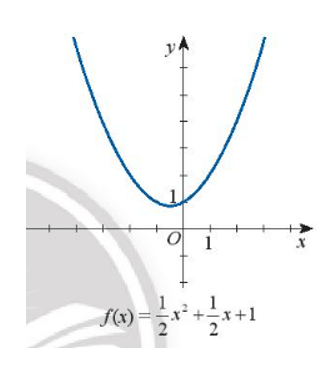
d) $\frac{1}{2}$ x² + $\frac{1}{2}$ x + 1 ≤ 0

Lời giải:

a)

Dựa vào hình vẽ ta thấy:

Đồ thị hàm số f(x) cắt trục hoành tại hai điểm có hoành độ lần lượt là x₁ = -3 và x₂ = $\frac{1}{2}$ hay với x₁ = -3 và x₂ = $\frac{1}{2}$ thì f(x) = 0.

Trong hai khoảng (-∞; - 3) và $\left(\frac{1}{2};+\infty \right)$ đồ thị hàm số f(x) nằm phía trên trục hoành hay f(x) > 0 khi x thuộc hai khoảng (-∞; - 3) và $\left(\frac{1}{2};+\infty \right)$ .

Trong khoảng $\left(-3;\frac{1}{2}\right)$ đồ thị hàm số f(x) nằm phía dưới trục hoành hay f(x) < 0 khi x thuộc khoảng $\left(-3;\frac{1}{2}\right)$ .

Vậy bất phương trình x² + 2,5x – 1,5 ≤ 0 có tập nghiệm là .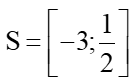

b)

Dựa vào hình vẽ ta thấy:

Đồ thị hàm số f(x) cắt trục hoành tại một điểm có hoành độ x = -4 hay f(x) = 0 khi x = -4.

Với x ≠ -4 thì đồ thị hàm số f(x) nằm phía dưới trục hoành nên f(x) < 0 với x ≠ -4.

Vậy bất phương trình – x² – 8x – 16 < 0 có tập nghiệm là S = ℝ\{-4}.

c)

Dựa vào hình vẽ ta thấy:

Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt x₁ = $\frac{3}{2}$ và x₂ = 4 hay f(x) = 0 khi x₁ = $\frac{3}{2}$ và x₂ = 4.

Đồ thị hàm số f(x) nằm phía dưới trục hoành với x thuộc hai khoảng $\left(-\infty ;\frac{3}{2}\right)$ và (4; +∞) hay f(x) < 0 với x thuộc $\left(-\infty ;\frac{3}{2}\right)$ ∪ (4; +∞).

Đồ thị hàm số f(x) nằm phía trên trục hoành với x thuộc khoảng $\left(\frac{3}{2};4\right)$ hay f(x) > 0 với x thuộc khoảng $\left(\frac{3}{2};4\right)$ .

Vậy bất phương trình – 2x² + 11x – 12 > 0 có tập nghiệm S = $\left(\frac{3}{2};4\right)$ .

d)

Dựa vào hình vẽ ta thấy:

Đồ thi hàm số f(x) nằm phía trên trục hoành với mọi x hay f(x) > 0 với x ∈ ℝ.

Vậy bất phương trình $\frac{1}{2}$x² + $\frac{1}{2}$x + 1 ≤ 0 có tập nghiệm S = $\varnothing$.

Lời giải bài tập Toán lớp 10 Bài 2: Giải bất phương trình bậc hai một ẩn Chân trời sáng tạo hay khác:

• Giải Toán 10 trang 11 Tập 2

• Giải Toán 10 trang 13 Tập 2