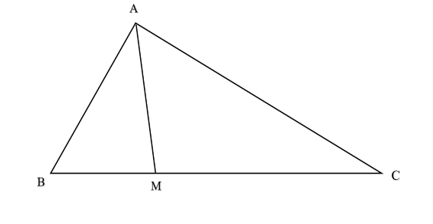
Cho tam giác ABC có AB = 4, BC = 6, AC = 2 căn bậc hai 7 . Điểm M thuộc đoạn BC
Câu hỏi:
A.
B. 3
C.
D.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
Đặt AB = c = 4, AC = b = 2 , BC = a = 6.
Áp dụng định lí côsin cho tam giác ABC:
b2 = a2 + c2 – 2accosB
⇒ cosB =
⇒ cosB =
BC = 6 và MC = 2MB ⇒ MC = 4 và MB = 2.
Áp dụng định lí côsin cho tam giác ABM:
AM2 = AB2 + BM2 – 2.AM.BM.cos
AM2 = 42 + 22 – 2.2.4.
AM =
Vậy đáp án đúng là C.