Cho tam giác ABC, có AB = 5, AC = 8 và góc A = 45 độ. Tính độ dài các cạnh và độ lớn
Câu hỏi:
Trả lời:
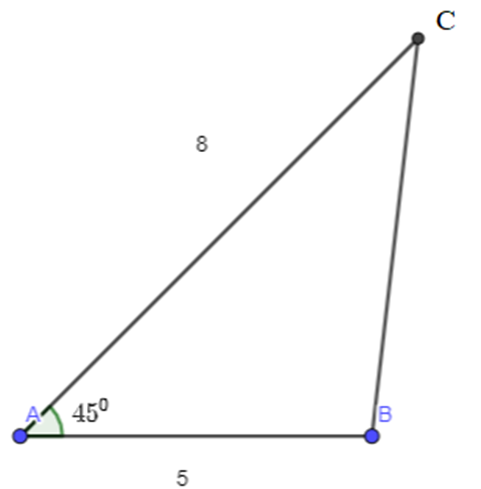
Xét tam giác ABC:
Theo định lí cosin, ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
BC2 = 52 + 82 – 2.5.8.cos450
BC2 =
BC ≈ 5,7 cm.
Ta có:
Câu hỏi:
Trả lời:

Xét tam giác ABC:
Theo định lí cosin, ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
BC2 = 52 + 82 – 2.5.8.cos450
BC2 =
BC ≈ 5,7 cm.
Ta có:
Câu 1:
Ngắm Tháp Rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí ta đứng tới Tháp Rùa. Em có biết vì sao?

Câu 2:
Một tàu biển xuất phát từ cảng Vân Phong (Khánh Hòa) theo hướng đông với vận tốc 20km/h. Sau khi đi được 1 giờ, tàu chuyển sang hướng Đông Nam rồi giữ nguyên vận tốc và đi tiếp.
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilômét (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng Định lí Pythagore (Pi – ta – go) để tính chính xác các số đo trong câu b hay không?
Câu 3:
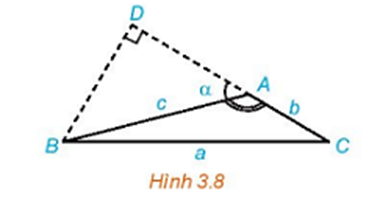
Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A.
a) Tính a2 theo BD2 và CD2.
b) Tính a2 theo b, c và DA.
c) Tính DA theo c và cosA.
d) Chứng minh a2 = b2 + c2 – 2bc.cosA.
Câu 4:
Định lý Pythagore có phải là một trường hợp đặc biệt của định lý côsin hay không?
Câu 5:
Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số đo góc A và kiểm tra tính đúng đắn của Định lí Côsin tại đỉnh A đối với tam giác đó.
Câu 8:
Cho tam giác ABC có b = 8, c = 5 và . Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.
