Một chiếc hộp đựng 6 viên bi trắng, 4 viên bi đỏ và 2 viên bi đen. Chọn ngẫu nhiên ra 6 viên bi. Tính xác suất để trong 6 viên bi đó có 3 viên bi trắng, 2 viên bi đỏ và 1 viên bi đen.

A. Các câu hỏi trong bài

Trở lại tình huống mở đầu trong Bài 26. Hãy tính xác suất trúng giải độc đắc, giải nhất của bạn An khi chọn bộ số {5; 13; 20; 31; 32; 35}.

Theo định nghĩa cổ điển của xác suất để tính xác suất của biến cố F: “Bạn An trúng giải độc đắc” và biến cố G: “Bạn An trúng giải nhất” ta cần xác định n(Ω), n(F) và n(G). Liệu có thể tính n(Ω), n(F) và n(G) bằng cách liệt kê ra hết các phần tử của Ω, F và G rồi kiểm đếm được không.

Một tổ trong lớp 10B có 12 học sinh, trong đó có 7 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 6 học sinh trong tổ để kiểm tra vở bài tập Toán. Tính xác suất để trong 6 học sinh được chọn số học sinh nữ bằng số học sinh nam.

Trong trò chơi "Vòng quay may mắn", người chơi sẽ quay hai bánh xe. Mũi tên ở bánh xe thứ nhất có thể dừng ở một trong hai vị trí: Loại xe 50 cc và Loại xe 110 cc. Mũi tên ở bánh xe thứ hai có thể dừng ở một trong bốn vị trí: màu đen, màu trắng, màu đỏ và màu xanh. Vị trí của mũi tên trên hai bánh xe sẽ xác định người chơi nhận được loại xe nào, màu gì.

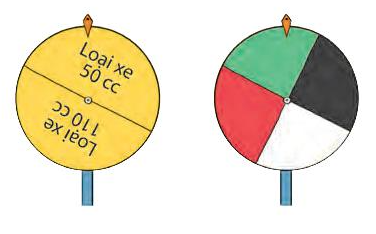
Phép thử T là quay hai bánh xe. Hãy vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

Gieo liên tiếp một con xúc xắc cân đối và một đồng xu cân đối.

a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

b) Tính xác suất của các biến cố sau:

F: “Đồng xu xuất hiện mặt ngửa”;

G: “Đồng xu xuất hiện mặt sấp hoặc số chấm xuất hiện trên con xúc xắc là 5”. 

Trên một phố có hai quán ăn X, Y. Ba bạn Sơn, Hải, Văn mỗi người chọn ngẫu nhiên một quán ăn.

a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

b) Tính xác suất của biến cố “Hai bạn vào quán X, bạn còn lại vào quán Y”.

Màu hạt của đậu Hà Lan có hai kiểu hình là màu vàng và màu xanh tương ứng với hai loại gene là gene trội A và gene lặn a. Hình dạng hạt của đậu Hà Lan có hai kiểu hình là hạt trơn và hạt nhăn tương ứng với hai loại gene là gene trội B và gene lặn b. Biết rằng, cây con lấy ngẫu nhiên một gene từ cây bố và một gene từ cây mẹ.

Phép thử là cho lai hai loại đậu Hà Lan, trong đó cả cây bố và cây mẹ đều có kiểu gene là (Aa, Bb) và kiểu hình là hạt màu vàng và trơn. Giả sử các kết quả có thể là đồng khả năng. Tính xác suất để cây con cũng có kiểu hình là hạt màu vàng và trơn.