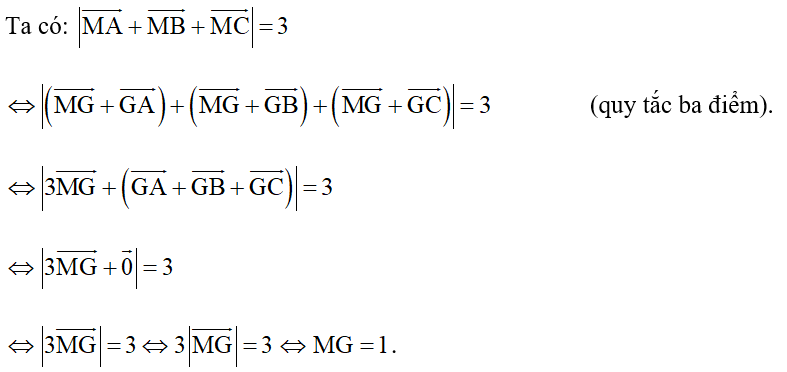Giải Toán 10 trang 95 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 95 Tập 2 trong Bài tập ôn tập cuối năm Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 95.

Giải Toán 10 trang 95 Tập 2 Kết nối tri thức

Bài 1 trang 95 Toán 10 Tập 2: Cho hệ bất phương trình bậc nhất hai ẩn $\left\{\begin{array}{l}x+y>2\\ x-y\le 1\end{array}\right.$. Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?

A. (1; 1). 

B. (2; 0). 

C. (3; 2). 

D. (3; – 2).

Lời giải:

Đáp án đúng là: C. 

Ta có: $\left\{\begin{array}{l}x+y>2\left(1\right)\\ x-y\le 1\left(2\right)\end{array}\right.$

Lần lượt thay tọa độ của các điểm vào hệ bất phương trình đã cho và xét xem tọa độ điểm nào thỏa mãn. 

+ Đáp án A: Ta có 1 + 1 > 2 (vô lí) nên điểm (1; 1) không thỏa mãn bất phương trình (1), do đó điểm (1; 1) không thuộc miền nghiệm của bất phương trình đã cho. 

+ Đáp án B: Ta có 2 + 0 > 2 (vô lí) nên điểm (2; 0) không thỏa mãn bất phương trình (1), do đó điểm (2; 0) không thuộc miền nghiệm của bất phương trình đã cho. 

+ Đáp án C: Ta có 3 + 2 > 2 và 3 – 2 ≤ 1 (luôn đúng) nên điểm (3; 2) thỏa mãn của hai bất phương trình (1) và (2), do đó điểm (3; 2) thuộc miền nghiệm của bất phương trình đã cho. 

+ Đáp án D: Ta có 3 + (– 2) > 2 (vô lý) nên điểm (3; – 2) không thỏa mãn bất phương trình (1), do đó điểm (3; – 2) không thuộc miền nghiệm của bất phương trình đã cho. 

Bài 2 trang 95 Toán 10 Tập 2: Cho tam giác ABC. Có bao nhiêu điểm M thỏa mãn $\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|$ = 3?

A. Vô số.

B. 1.

C. 2.

D. 3.

Lời giải:

Đáp án đúng là: A.

Gọi G là trọng tâm của tam giác ABC.

Do đó, $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ (tính chất trọng tâm của tam giác).

Vậy, tập hợp các điểm M thỏa mãn yêu cầu đề bài là đường tròn tâm G bán kính 1.

Do đó có vô số điểm M thỏa mãn.

Bài 3 trang 95 Toán 10 Tập 2: Biết rằng parabol y = x² + bx + c có đỉnh là I(1; 4). Khi đó giá trị của b + c là

A. 1.                    

B. 2.                   

C. 3.                      

D. 4.

Lời giải:

Đáp án đúng là: C.

Parabol có đỉnh là I(1; 4) nên $\frac{-b}{2.1}=1\iff b=-2$. 

Tọa độ điểm I(1; 4) thỏa mãn phương trình y = x² + bx + c, thay tọa độ I vào ta được: 

4 = 1² + (– 2) . 1 + c ⇔ c = 5. 

Do đó: b + c = – 2 + 5 = 3. 

Bài 4 trang 95 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x + 2y – 5 = 0. Tìm mệnh đề sai trong các mệnh đề sau:

A. Vectơ $\overrightarrow{n}=\left(1;2\right)$ là một vectơ pháp tuyến của Δ.

B.  Vectơ $\overrightarrow{u}=\left(2;-1\right)$ là một vectơ chỉ phương của Δ.

C. Đường thẳng Δ song song với đường thẳng d: $\left\{\begin{array}{l}x=1-2t\\ y=1+t\end{array}\right.$.

D. Đường thẳng Δ có hệ số góc k = 2.

Lời giải:

Đáp án đúng là: D.

Ta có phương trình đường thẳng Δ: x + 2y – 5 = 0. 

Một vectơ pháp tuyến của đường thẳng ∆ là $\overrightarrow{n}=\left(1;2\right)$, do đó, một vectơ chỉ phương của ∆ là $\overrightarrow{u}=\left(2;-1\right)$. 

Vậy đáp án A, B đúng. 

Đường thẳng d: $\left\{\begin{array}{l}x=1-2t\\ y=1+t\end{array}\right.$ có một vectơ chỉ phương là $\overrightarrow{u_d}=\left(-2;1\right)$ và đi qua điểm A(1; 1). 

Vì 1 + 2 . 1 – 5 = – 2 ≠ 0, do đó A(1; 1) không thuộc đường thẳng ∆. 

Do đó, hai đường thẳng ∆ và d có cùng vectơ chỉ phương, có điểm A thuộc d nhưng không thuộc ∆, vậy d // ∆. 

Vậy đáp án C đúng. 

Ta có: x + 2y – 5 = 0 ⇔ y = $-\frac{1}{2}x+\frac{5}{2}$. 

Do đó hệ số góc của ∆ là k = $-\frac{1}{2}$. 

Vậy đáp án D sai. 

Bài 5 trang 95 Toán 10 Tập 2: Trong khai triển nhị thức Newton của (2 + 3x)⁴, hệ số của x² là:

A. 9.                   

B. $C_4^2$.                 

C. $9C_4^2$.                      

D. $36C_4^2$. 

Lời giải:

Đáp án đúng là: D.

Áp dụng công thức nhị thức Newton, ta có: 

(2 + 3x)⁴ = $C_4^0$. 2⁴ + $C_4^1$. 2³ . 3x + $C_4^2$. 2² . (3x)² + $C_4^3$. 2 . (3x)³ + $C_4^4$. (3x)⁴

= 16 + 24x$C_4^1$ + 36$C_4^2$x² + 54$C_4^3$x³ + 81x⁴
Hệ số của x² trong khai triển của (2 + 3x)⁴ là 36$C_4^2$. 

Bài 6 trang 95 Toán 10 Tập 2: Xác suất để trong hai người được chọn có ít nhất một nữ là:

A. $\frac{7}{15}$. 

B. $\frac{8}{15}$. 

C. $\frac{1}{15}$. 

D. $\frac{2}{15}$. 

Lời giải:

Đáp án đúng là: B. 

Tổ đó có tất cả: 7 + 3 = 10 (bạn). 

Chọn ngẫu nhiên 2 người trong 10 người, có $C_{10}^2=45$ cách chọn hay n(Ω) = 45. 

Gọi biến cố A: “Chọn được 2 người có  ít nhất 1 nữ”. 

Để chọn được hai người, trong đó có ít nhất 1 nữ, ta xét hai trường hợp sau: 

+ Trường hợp 1, chọn 1 nữ và 1 nam:

Chọn 1 nữ trong 3 nữ có $C_3^1=3$ cách chọn. 

Chọn 1 nam trong 7 nam có $C_7^1=7$ cách chọn. 

Theo quy tắc nhân, có 3 . 7 = 21 cách chọn 1 nữ, 1 nam. 

+ Trường hợp 1, chọn 2 nữ:

Chọn 2 nữ trong 3 nữ có $C_3^2=3$ cách chọn. 

Theo quy tắc cộng, có 21 + 3 = 24 cách chọn đẻ chọn được 2 người có ít nhất một nữ. 

Do đó, n(A) = 24. 

Vậy xác suất để chọn được 2 người có ít nhất một nữ là P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{24}{45}=\frac{8}{15}$.

Bài 7 trang 95 Toán 10 Tập 2: Cho các mệnh đề:

P: “Tam giác ABC là tam giác vuông tại A”;

Q: “Tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC²”.

a) Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q,$\overline{P}$ ⇒$\overline{Q}$. Xét tính đúng sai của các mệnh đề này.

b) Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.

c) Gọi X là tập hợp các tam giác ABC vuông tại A, Y là tập hợp các tam giác ABC có trung tuyến AM = $\frac{1}{2}$BC. Nêu mối quan hệ giữa hai tập hợp X và Y.

Lời giải:

a) Phát biểu các mệnh đề và xét tính đúng sai của mỗi mệnh đề như sau: 

+) P ⇒ Q: “Nếu tam giác ABC là tam giác vuông tại A thì tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC²”. Mệnh đề này là mệnh đề đúng (theo định lý Pythagore).

+) Q ⇒ P: “Nếu tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC² thì tam giác ABC là tam giác vuông tại A”. Mệnh đề này là mệnh đề đúng (theo định lý Pythagore).

+) P ⇔ Q: “Tam giác ABC là tam giác vuông tại A khi và chỉ khi tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC²”. Mệnh đề P ⇔ Q là mệnh đề đúng (Vì P ⇒ Q và Q ⇒ P đúng).

+)$\overline{P}$ ⇒ $\overline{Q}$: “Nếu tam giác ABC không là tam giác vuông tại A thì tam giác ABC có các cạnh thỏa mãn AB² + AC² ≠ BC²”. Mệnh đề này là mệnh đề đúng. 

b) 

+) Tam giác ABC là tam giác vuông tại A là điều kiện đủ để tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC².

+) Tam giác ABC có các cạnh thỏa mãn AB² + AC² = BC² là điều kiện cần để tam giác ABC là tam giác vuông tại A.

c) Ta biết rằng một tam giác là vuông khi và chỉ khi đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. 

Do đó, nếu tam giác ABC có trung tuyến AM = $\frac{1}{2}$BC thì tam giác ABC vuông tại A.

Vậy mối quan hệ giữa hai tập hợp X và Y là X = Y.

Lời giải bài tập Toán lớp 10 Bài tập ôn tập cuối năm Kết nối tri thức hay khác:

• Giải Toán 10 trang 96

• Giải Toán 10 trang 97