Vận dụng 2 trang 9 Toán 10 Tập 2 - Kết nối tri thức
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.
Giải Toán lớp 10 Bài 15: Hàm số
Vận dụng 2 trang 9 Toán 10 Tập 2: Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.
a) Tính số tiền phải trả khi di chuyển 25 km.
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
Lời giải:
a) Khi di chuyển 25 km thì khách hàng phải trả 10 000 đồng cho 0,6 km đầu (giá mở cửa) và 13 000 đồng trên 1 km cho 25 – 0,6 = 24,4 km sau (giá tính cho km tiếp theo dưới 25 km).
Do đó tổng số tiền phải trả khi di chuyển 25 km là:
10 000 + 24,4 . 13 000 = 327 200 (đồng).
Vậy số tiền phải trả khi di chuyển 25 km là 327 200 đồng.
b) Gọi x (km, x > 0) là độ dài quãng đường di chuyển và y (đồng) là số tiền phải trả tương ứng.
Ta có:
+ Giá mở cửa là 10 000 đồng cho 0,6 km đầu, tức là khi x ≤ 0,6 thì số tiền phải trả tương ứng là y = 10 000.
+ Giá tiền cho km tiếp theo dưới 25 km là 13 000 đồng trên 1 km, tức là khi 0,6 < x < 25 thì số tiền phải tương ứng là y = 10 000 + 13 000(x – 0,6) hay y = 13 000x + 2 200.
+ Giá tiền phải trả cho km thứ 25 trở lên là 11 000 đồng trên 1 km, tức là khi x ≥ 25 thì số tiền phải trả tương ứng là y = 10 000 + 13 000 . 24,4 + 11 000(x – 25) hay y = 11 000 x + 52 200.
Vậy ta có công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển là:
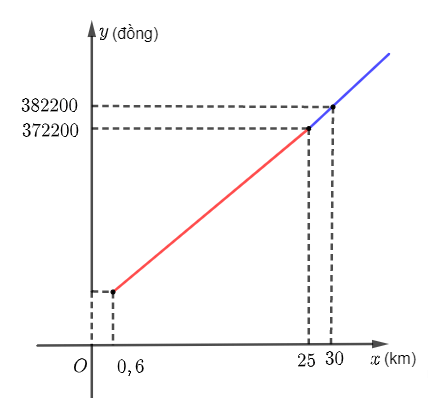
c) Ta vẽ đồ thị hàm số bằng cách vẽ các đồ thị y = 10 000 trên (0; 0,6], đồ thị y = 13 000x + 2 200 trên (0,6; 25) và đồ thị y = 11 000x + 52 200 trên [25; + ∞).
Đồ thị hàm số được vẽ như sau:
Quan sát hình, ta thấy đồ thị hàm số đi lên từ trái sang phải trên (0,6; + ∞). Vậy hàm số này đồng biến trên (0,6; + ∞).
Lời giải bài tập Toán 10 Bài 15: Hàm số hay, chi tiết khác:
HĐ3 trang 5 Toán 10 Tập 2: Tính tiền điện dựa vào Bảng 6.2 về giá bán lẻ điện sinh hoạt ....
Luyện tập 2 trang 7 Toán 10 Tập 2: Dựa vào đồ thị của hàm số (H.6.2), tìm x sao cho y = 8 ....