Hoạt động 2 trang 67 Toán 11 Tập 1 Cánh diều
Cho hàm số f(x) = x – 1, g(x) = x + 1.
Giải Toán 11 Bài 2: Giới hạn của hàm số - Cánh diều
Hoạt động 2 trang 67 Toán 11 Tập 1: Cho hàm số f(x) = x2 – 1, g(x) = x + 1.
a) f(x)và g(x).
b) và so sánh với .
c) và so sánh với .
d) và so sánh với .
e) và so sánh với .
Lời giải:
a) Giả sử (xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
-1 = 1-1 = 0.
limf(x) = 0.
limg(xn) = lim(xn+1) = limxn+1 = 2
limg(x) = 2.
b) Ta có: f(x) + g(x) = x2 – 1 + x + 1 = x2 + x
(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
.
.
Ta lại có: = 0 + 2 =2.
Vậy =2.
c) Ta có: f(x) – g(x) = x2 – 1 – x – 1 = x2 – x – 2
(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
.
Ta lại có: = 0-2 = -2.
Vậy = -2.
d) Ta có: f(x).g(x) = (x2 – 1)(x + 1) = x3 + x2 – x – 1
(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
-1 = 13+12-1-1 = 0
=0.
Ta lại có: = 0.2 = 0.
Vậy .
e) Ta có:
(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
= 0.
= 0.
Ta lại có: =0
Vậy .
Lời giải bài tập Toán 11 Bài 2: Giới hạn của hàm số hay, chi tiết khác:
Hoạt động 1 trang 65 Toán 11 Tập 1: Xét hàm số f(x) = 2x. a) Xét dãy số (xn), với xn = 1+ ....
Luyện tập 1 trang 67 Toán 11 Tập 1: Sử dụng định nghĩa, chứng minh rằng: =4 ....
Hoạt động 4 trang 69 Toán 11 Tập 1: Cho hàm số f(x) = (x0)có đồ thị như ở Hình 7 ....
Hoạt động 5 trang 70 Toán 11 Tập 1: Cho hàm số f(x) = có đồ thị như Hình 8 ....

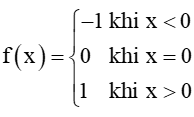 ....
....