Giải Toán 11 trang 113 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 113 Tập 1 trong Bài 5: Hình lăng trụ và hình hộp Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 113.

Giải Toán 11 trang 113 Tập 1 Cánh diều

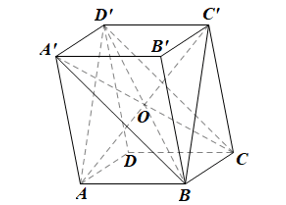
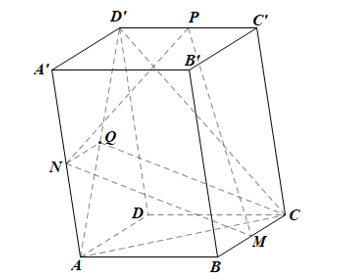
Luyện tập 3 trang 113 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng bốn mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’) cùng đi qua một điểm.

Lời giải:

Trong mặt phẳng (ABC’D’), xét tứ giác ABC’D’ có:

     AB // C’D’ (cùng song song với DC);

     AB = C’D’ (cùng bằng DC)

Do đó tứ giác ABC’D’ là hình bình hành.

Suy ra hai đường chéo AC’ và BD’ cắt nhau tại trung điểm O của mỗi đường.

Khi đó (ABC’D’) đi qua điểm O.

Tương tự ta cũng có tứ giác BCD’A’ là hình bình hành có hai đường chéo BD’ và CA’ cắt nhau tại trung điểm của mỗi đường.

Mà O là trung điểm của BD’, do đó O là trung điểm của CA’ và (BCD’A’) đi qua O.

Chứng minh tương tự với các mp(CDA’B’), (DAB’C’) thì các mặt phẳng này cũng đi qua điểm O.

Vậy bốn mặt phẳng (ABC’D’), (BCD’A’), (CDA’B’), (DAB’C’) cùng đi qua điểm, điểm O là giao điểm các đường chéo của hình hộp.

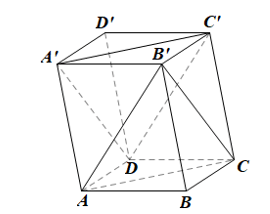
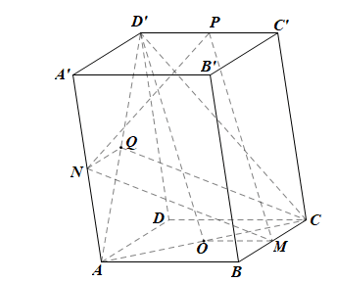
Bài 1 trang 113 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C D’.

a) Chứng minh rằng (ACB’) // (A’C’D).

b) Gọi G₁, G₂ lần lượt là giao điểm của BD’ với các mặt phẳng (ACB’) và (A’C’D). Chứng minh rằng G₁, G₂ lần lượt là trọng tâm của hai tam giác ACB’ và A’C’D.

c) Chứng minh rằng BG₁ = G₁G₂ = D’G₂.

Lời giải:

a)

Ta có: (ABCD) // (A’B’C’D’) ( do ABCD.A’B’C’D’ là hình hộp);

           (ABCD) ∩ (ACC’A’) = AC;

           (A’B’C’D’) ∩ (ACC’A’) = A’C’.

Do đó AC // A’C’.

Mà A’C’ ⊂ (A’C’D) nên AC // (A’C’D).

Chứng minh tương tự ta cũng có AB’ // DC’ mà DC’ ⊂ (A’C’D) nên AB’ // (A’C’D).

Ta có: AC // (A’C’D);

          AB’ // (A’C’D);

          AC, AB’ cắt nhau tại điểm A và cùng nằm trong mp(ACB’).

Do đó (ACB’) // (A’C’D).

b)

• Gọi O là tâm hình bình hành đáy ABCD, I là giao điểm của BD’ và DB’.

Tứ giác BDD’B’ có BB’ // DD’ và BB’ = DD’ nên là hình bình hành.

Do đó hai đường chéo BD’ và DB’ cắt nhau tại trung điểm I của mỗi đường.

Trong mp(BDD’B’), BD’ cắt B’O tại G₁.

Mà B’O ⊂ (ACB’) nên G₁ là giao điểm của BD’ với (ACB’).

Trong mp(BDD’B’), xét $∆$BDB’ có hai đường trung tuyến BI, B’O cắt nhau tại G₁ nên G₁ là trọng tâm của DBDB’

Do đó $\frac{B^{\text{'}}{G}_1}{BO}=\frac{2}{3}$

Trong (ACB’), xét $∆$ACB’ có B’O là đường trung tuyến và $\frac{B^{\text{'}}{G}_1}{BO}=\frac{2}{3}$

Suy ra G₁ là trọng tâm của $∆$ACB’.

• Gọi O’ là tâm hình bình hành đáy A’B’C’D’.

Chứng minh tương tự như trên ta cũng có: G₂ là trọng tâm của $∆$DD’B’ nên $\frac{D{G}_2}{D{O}^{\text{'}}}=\frac{2}{3}$

Trong (A’C’D), $∆$A’C’D có DO’ là đường trung tuyến và  $\frac{D{G}_2}{D{O}^{\text{'}}}=\frac{2}{3}$

Suy ra G₂ là trọng tâm của $∆$A’C’D.

c) Theo chứng minh câu b, ta có:

• G₁ là trọng tâm của $∆$BDB’ nên $\frac{B{G}_1}{BI}=\frac{2}{3}$  và $\frac{I{G}_1}{B{G}_1}=\frac{1}{2}$

• G₂ là trọng tâm của  $∆$DD’B’ nên $\frac{D^{\text{'}}{G}_2}{D^{\text{'}}I}=\frac{2}{3}$  và $\frac{I{G}_2}{D^{\text{'}}{G}_2}=\frac{1}{2}$

Do đó $\frac{B{G}_1}{BI}=\frac{D^{\text{'}}{G}_2}{D^{\text{'}}I}=\frac{2}{3}$  và $\frac{I{G}_1}{B{G}_1}=\frac{I{G}_2}{D^{\text{'}}{G}_2}=\frac{1}{2}$

Ta có: $\frac{B{G}_1}{BI}=\frac{D^{\text{'}}{G}_2}{D^{\text{'}}I}$ và BI = D’I (do I là trung điểm của BD’)

Suy ra BG₁ = D’G₂.

Lại có $\frac{I{G}_1}{B{G}_1}=\frac{I{G}_2}{D^{\text{'}}{G}_2}=\frac{1}{2}$  nên IG₁ = IG₂ = $\frac{1}{2}$ BG₁

Do đó G₁G₂ = IG₁ + IG₂ = $\frac{1}{2}$ BG₁ + $\frac{1}{2}$ BG₁ = BG₁.

Vậy BG₁ = G₁G₂ = D’G₂.

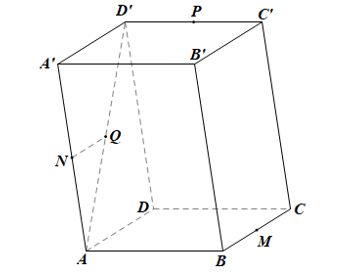
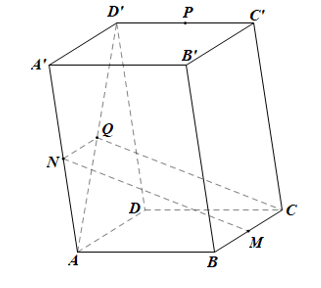
Bài 2 trang 113 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA’, C’D’, AD’. Chứng minh rằng:

a) NQ // A’D’ và NQ = $\frac{1}{2}$ A’D’;

b) Tứ giác MNQC là hình bình hành;

c) MN // (ACD’);

d) (MNP) // (ACD’).

Lời giải:

a)

Trong mp(ADD’A’), xét DAA’D’ có N, Q lần lượt là trung điểm của AA’ và AD’

Do đó NQ là đường trung bình của tam giác

Suy ra NQ // A’D’ và NQ = $\frac{1}{2}$ A’D’.

b)

Ta có: A’D’ // AD // BC, mà NQ // A’D’ (câu a) nên NQ // BC hay NQ // MC.

Ta cũng có A’D’ = AD = BC, mà NQ = $\frac{1}{2}$ A’D’ (câu a) nên NQ = $\frac{1}{2}$ BC

Lại có BM = MC = $\frac{1}{2}$ BC (do M là trung điểm BC)

Do đó NQ = MC.

Tứ giác MNQC có NQ // MC và NQ = MC nên là MNQC hình bình hành.

c)

Do MNQC hình bình hành nên MN // QC

Mà QC ⊂ (ACD’) nên MN // (ACD’).

d)

Gọi O là trung điểm của ABCD.

Trong (ABCD), xét DABC có O, M lần lượt là trung điểm của AC, BC nên OM là đường trung bình của tam giác

Do đó OM // AB và OM = $\frac{1}{2}$ AB.

Mà AB // D’P nên OM // D’P.

Lại có D’P = $\frac{1}{2}$ D’C’ và D’C’ = AB nên OM = D’P.

Xét tứ giác D’PMO có OM // D’P và OM = D’P nên là hình bình hành

Suy ra PM // D’O

Mà D’O ⊂ (ACD’) nên PM // (ACD’).

Ta có: MN // (ACD’);

           PM // (ACD’);

           MN, PM cắt nhau tại điểm M và cùng nằm trong mp(MNP)

Do đó (MNP) // (ACD’).

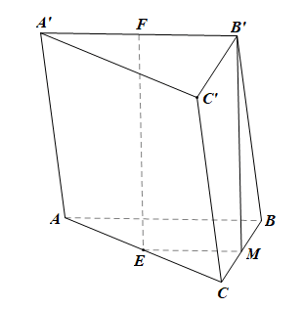
Bài 3 trang 113 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi E, F lần lượt là trung điểm của các cạnh AC và A’B’.

a) Chứng minh rằng EF // (BCC’B’).

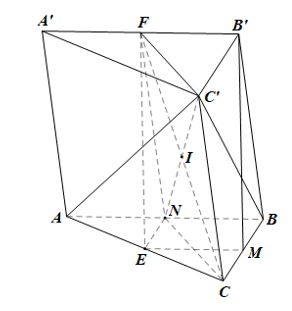
b) Gọi I là giao điểm của đường thẳng CF với mặt phẳng (AC’B). Chứng minh rằng I là trung điểm đoạn thẳng CF.

Lời giải:

a)

Gọi M là trung điểm của BC.

Trong mp(ABC), xét $∆$ABC có E, M lần lượt là trung điểm của AC, BC nên EM là đường trung bình của tam giác

Do đó EM // AB và EM = $\frac{1}{2}$ AB.

Mà AB // A’B’ nên EM // A’B’ hay EM // FB’.

Lại có AB = A’B’ và FB’ = $\frac{1}{2}$ A’B’ nên EM = FB’.

Trong mp(EMB’F), xét tứ giác EMB’F có EM // FB’ và EM = FB’ nên là hình bình hành.

Do đó EF // B’M, mà B’M ⊂ (BCC’B’) nên EF // (BCC’B’).

b)

Gọi N là trung điểm của AB.

Trong mp(ABB’A’), xét hình bình hành ABB’A’ cũng là hình thang có N, F lần lượt là trung điểm của AB, A’B’ nên NF là đường trung bình của hình thang

Do đó NF // BB’ và $NF=\frac{A{A}^{\text{'}}+B{B}^{\text{'}}}{2}=\frac{2B{B}^{\text{'}}}{2}=B{B}^{\text{'}}$ .

Mà BB’ // CC’ nên NF // CC’.

Lại có BB’ = CC’ nên NF = CC’.

Trong mp(NFC’C), xét tứ giác NFC’C có NF // CC’ và NF = CC’ nên là hình bình hành.

Do đó hai đường chéo CF và NC’ cắt nhau tại trung điểm của mỗi đường.

Lại có NC’ ⊂ (ABC’) nên CF cắt (ABC’) tại trung điểm I của CF.

Vậy CF cắt (ABC’) tại trung điểm I của CF.

Lời giải bài tập Toán 11 Bài 5: Hình lăng trụ và hình hộp hay khác:

• Giải Toán 11 trang 110
• Giải Toán 11 trang 111
• Giải Toán 11 trang 112