Giải Toán 11 trang 120 Tập 1 Cánh diều
Với Giải Toán 11 trang 120 Tập 1 trong Bài tập cuối chương 4 Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 120.
Giải Toán 11 trang 120 Tập 1 Cánh diều
Bài 1 trang 120 Toán 11 Tập 1: Trong không gian, hai đường thẳng song song với nhau khi và chỉ khi:
A. Hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.
B. Hai đường thẳng không có điểm chung.
C. Hai đường thẳng cùng nằm trong một mặt phẳng.
D. Hai đường thẳng cùng song song với đường thẳng thứ ba.
Lời giải:
Đáp án đúng là: A
Trong không gian, hai đường thẳng song song với nhau khi và chỉ khi hai đường thẳng cùng nằm trong một mặt phẳng và không có điểm chung.
Bài 2 trang 120 Toán 11 Tập 1: Cho hai đường thẳng phân biệt a và b trong không gian. Có bao nhiêu vị trí tương đối giữa a và b?
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải:
Đáp án đúng là: C
Có 3 vị trí tương đối giữa hai đường thẳng phân biệt a và b:
• a và b cắt nhau tại 1 điểm;
• a và b song song với nhau;
• a và b chéo nhau.
Bài 3 trang 120 Toán 11 Tập 1: Trong không gian, đường thẳng song song với mặt phẳng khi và chỉ khi:
A. Đường thẳng đó song song với một đường thẳng thuộc mặt phẳng.
B. Đường thẳng và mặt phẳng không có điểm chung.
C. Đường thẳng đó không có điểm chung với một đường thẳng thuộc mặt phẳng.
D. Đường thẳng đó không có điểm chung với hai đường thẳng thuộc mặt phẳng.
Lời giải:
Đáp án đúng là: B
Đường thẳng được gọi là song song với mặt phẳng nếu chúng không có điểm chung.
Bài 4 trang 120 Toán 11 Tập 1: Trong không gian, hai mặt phẳng song song với nhau khi và chỉ khi:
A. Có một mặt phẳng chứa hai đường thẳng phân biệt cùng song song với mặt phẳng còn lại.
B. Hai mặt phẳng cùng song song với một đường thẳng.
C. Hai mặt phẳng cùng song song với mặt phẳng thứ ba.
D. Hai mặt phẳng không có điểm chung.
Lời giải:
Đáp án đúng là: D
Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung.
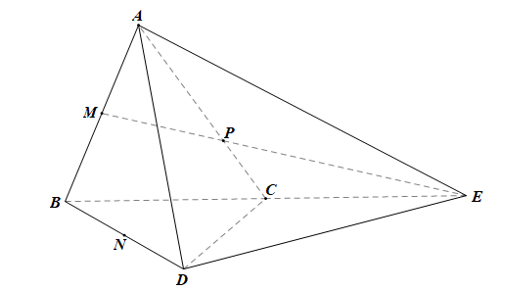
Bài 5 trang 120 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, BD. Điểm P thuộc cạnh AC sao cho PA = 2PC.
a) Xác định giao điểm E của đường thẳng MP với mặt phẳng (BCD).
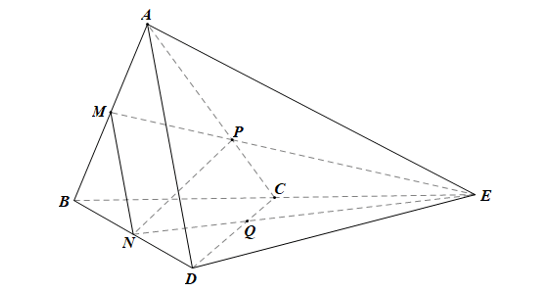
b) Xác định giao điểm Q của đường thẳng CD với mặt phẳng (MNP).
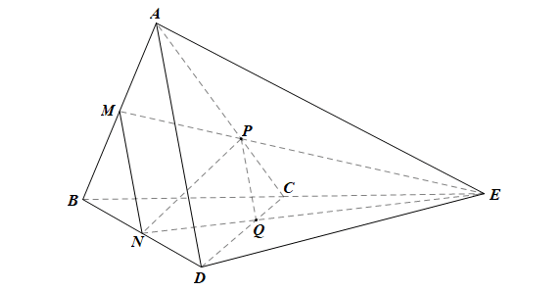
c) Xác định giao tuyến của mặt phẳng (ACD) với mặt phẳng (MNP).
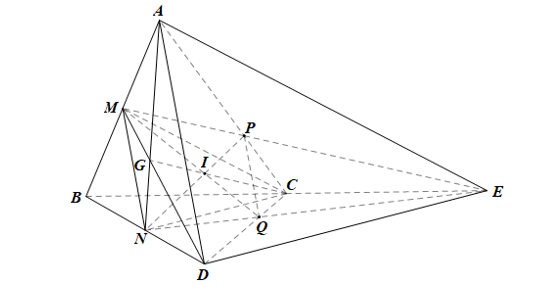
d) Gọi I là giao điểm của MQ và NP, G là trọng tâm của tam giác ABD. Chứng minh rằng C, I, G thẳng hàng.
Lời giải:
a)
Trong mp(ABC), kéo dài MP cắt BC tại E. Nối AE, DE.
Ta có: MP ∩ BC = {E};
BC ⊂ (BCD)
Do đó MP ∩ (BCD) = {E}.
b)
Nối NE, NE cắt CD tại Q.
Ta có: CD ∩ NE = {Q};
NE ⊂ (MNP)
Do đó CD ∩ (MNP) = {Q}.
c)
Ta có: P ∈ AC, mà AC ⊂ (ACD) nên P ∈ (ACD);
Mà P ∈ (MNP) nên P là giao điểm của (ACD) và (MNP).
Lại có Q ∈ CD và CD ⊂ (ACD) nên Q ∈ (ACD);
Mà Q ∈ (MNP) nên Q là giao điểm của (ACD) và (MNP).
Do đó PQ là giao tuyến của hai mặt phẳng (ACD) và (MNP).
d)
Do G là trọng tâm của tam giác ABD nên hai đường trung tuyến DM, AN của tam giác cùng đi qua G.
Ta có: G ∈ AN mà AN ⊂ (ANC) nên G ∈ (ANC);
G ∈ DM mà DM ⊂ (MDC) nên G ∈ (MDC).
Do đó G là giao điểm của hai mặt phẳng (ANC) và (MDC).
Lại có: C ∈ (ANC) và C ∈ (MDC) nên C cũng là giao điểm của hai mặt phẳng (ANC) và (MDC).
Vậy GC là giao tuyến của hai mặt phẳng (ANC) và (MDC).
Mặt khác, I là giao điểm của MQ và NP nên I ∈ MQ và I ∈ NP.
Vì I ∈ MQ mà MQ ⊂ (MDC) nên I ∈ (MDC)
Vì I ∈ NP mà NP ⊂ (ANC) nên I ∈ (ANC)
Do đó giao tuyến GC của hai mặt phẳng (ANC) và (MDC) đi qua điểm I.
Vậy ba điểm C, I, G thẳng hàng.
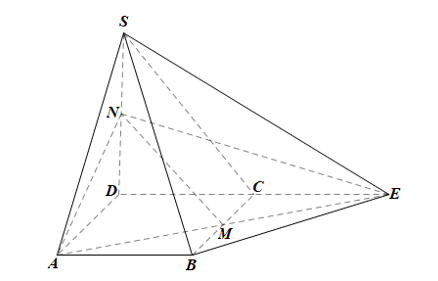
Bài 6 trang 120 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, SD. Xác định giao tuyến của mặt phẳng (AMN) với mỗi mặt phẳng sau:
a) (SCD);
b) (SBC).
Lời giải:
a)
Trong mp(ABCD), kéo dài AM cắt DC tại E. Nối SE, BE.
Ta có: E ∈ AM mà AM ⊂ (AMN) nên E ∈ (AMN);
E ∈ DC mà DC ⊂ (SCD) nên E ∈ (SCD).
Do đó E là giao điểm của hai mặt phẳng (AMN) và (SCD).
Lại có: N ∈ SD và SD ⊂ (SCD) nên N ∈ (SCD).
Mà N ∈ (AMN), nên N cũng là giao điểm của hai mặt phẳng (AMN) và (SCD).
Vậy (AMN) ∩ (SCD) = NE.
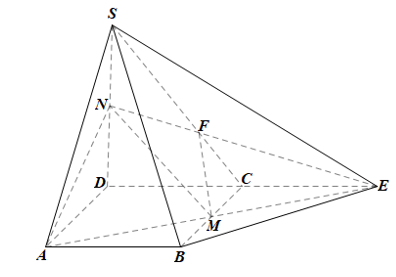
b)
Trong mp(SCD), gọi F là giao điểm của SC và NE.
Ta có: F ∈ NE mà NE ⊂ (AMN) nên F ∈ (AMN);
F ∈ SC mà SC ⊂ (SBC) nên F ∈ (SBC).
Do đó F là giao điểm của (AMN) và (SBC).
Lại có: M ∈ BC và BC ⊂ (SBC) nên M ∈ (SBC).
Mà M ∈ (AMN), nên M cũng là giao điểm của hai mặt phẳng (AMN) và (SBC).
Vậy (AMN) ∩ (SBC) = MF.
Lời giải bài tập Toán 11 Bài tập cuối chương 4 hay khác: