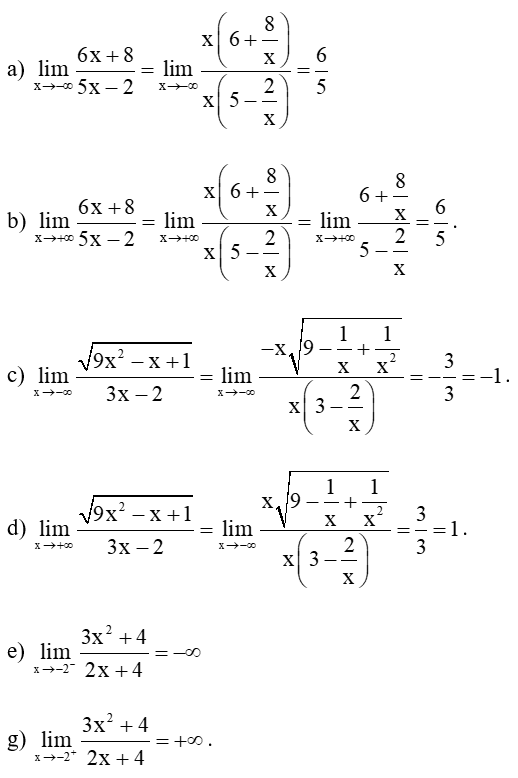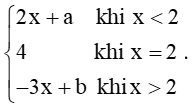Giải Toán 11 trang 79 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 79 Tập 1 trong Bài tập cuối chương 3 Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 79.

Giải Toán 11 trang 79 Tập 1 Cánh diều

Bài 1 trang 79 Toán 11 Tập 1: Cho hàm số y = f(x) xác định trên khoảng (a; b) và x₀ ∈ (a; b). Điều kiện cần và đủ để hàm số y = f(x) liên tục tại x₀ là:

A. $\underset{x\to x_0^{+}}{\lim }f\left(x\right)=f\left(x_0\right)$;

B. $\underset{x\to x_0^{-}}{\lim }f\left(x\right)=f\left(x_0\right)$;

C. $\underset{x\to x_0^{+}}{\lim }f\left(x\right)=\underset{x\to x_0^{-}}{\lim }f\left(x\right)$;

D. $\underset{x\to x_0^{+}}{\lim }f\left(x\right)=\underset{x\to x_0^{-}}{\lim }f\left(x\right)=f\left(x_0\right)$.

Lời giải:

Theo lí thuyết ta chọn đáp án D

Bài 2 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:

a) lim$\frac{2n^2+6n+1}{8n^2+5}$;

b) lim$\frac{4n^2-3n+1}{3n^3+6n^2-2}$;

c) lim$\frac{\sqrt{4n^2-n+3}}{8n-5}$;

d) lim$\left(4-\frac{2^{n+1}}{3^n}\right)$;

e) lim$\frac{{4.5}^n+2^{n+2}}{{6.5}^n}$;

g) lim$\frac{2+\frac{4}{n^3}}{6^n}$.

Lời giải:

Bài 3 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:

a) $\underset{x\to -3}{\lim }\left(4x^2-5x+6\right)$;

b) $\underset{x\to 2}{\lim }\frac{2x^2-5x+2}{x-2}$;

c) $\underset{x\to 4}{\lim }\frac{\sqrt{x}-2}{x^2-16}$.

Lời giải:

a) $\underset{x\to -3}{\lim }\left(4x^2-5x+6\right)=4{\left(-3\right)}^2$-5.(-3)+6 = -3.

b) $\underset{x\to 2}{\lim }\frac{2x^2-5x+2}{x-2}=\underset{x\to 2}{\lim }\frac{\left(x-2\right)\left(2x-1\right)}{x-2}=\underset{x\to 2}{\lim }\left(2x-1\right)=3$.

c) $\underset{x\to 4}{\lim }\frac{\sqrt{x}-2}{x^2-16}=\underset{x\to 4}{\lim }\frac{\sqrt{x}-2}{\left(x-4\right)\left(x+4\right)}=\underset{x\to 4}{\lim }\frac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\left(x+4\right)}$

$=\underset{x\to 4}{\lim }\frac{1}{\left(\sqrt{x}+2\right)\left(x+4\right)}=\frac{1}{32}$

Bài 4 trang 79 Toán 11 Tập 1: Tính các giới hạn sau:

a) $\underset{x\to -\infty }{\lim }\frac{6x+8}{5x-2}$;

b) $\underset{x\to +\infty }{\lim }\frac{6x+8}{5x-2}$;

c) $\underset{x\to -\infty }{\lim }\frac{\sqrt{9x^2-x+1}}{3x-2}$;

d) $\underset{x\to +\infty }{\lim }\frac{\sqrt{9x^2-x+1}}{3x-2}$;

e) $\underset{x\to -2^{-}}{\lim }\frac{3x^2+4}{2x+4}$;

g) $\underset{x\to -2^{+}}{\lim }\frac{3x^2+4}{2x+4}$.

Lời giải:

Bài 5 trang 79 Toán 11 Tập 1: Cho hàm số f(x) =

a) Với a = 0, b = 1, xét tính liên tục của hàm số tại x = 2.

b) Với giá trị nào của a, b thì hàm số liên tục tại x = 2?

c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định?

Lời giải:

a) Với a = 0, b = 1, hàm số f(x) =

Với x < 2 thì f(x) = 2x là hàm liên tục.

Với x > 2 thì f(x) = – 3x + 1 là hàm liên tục.

Tại x = 2 ta có:

$\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{-}}{\lim }2x=4$, $\underset{x\to 2^{+}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }\left(-3x+1\right)=-5$.

Suy ra $\underset{x\to 2^{-}}{\lim }f\left(x\right)\ne \underset{x\to 2^{+}}{\lim }f\left(x\right)$. Do đó không tồn tại $\underset{x\to 2}{\lim }f\left(x\right)$.

Vậy hàm số tiên tục trên ( – ∞; 2) và (2; +∞).

b) Ta có:

$\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{-}}{\lim }\left(2x+a\right)=4+a$, $\underset{x\to 2^{+}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }\left(-3x+b\right)=-6+b$

Để hàm số liên tục tại x = 2 thì:

$\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{+}}{\lim }f\left(x\right)=f\left(2\right)$.

Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.

c) Tập xác định của hàm số là: ℝ.

Để hàm số liên tục trên ℝ thì hàm số liên tục tại x = 2. Vì vậy với a = 0 và b = 10 thỏa mãn điều kiện.

Lời giải bài tập Toán 11 Bài tập cuối chương 3 Cánh diều hay khác:

• Giải Toán 11 trang 80