Giải Toán 11 trang 94 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 94 Tập 1 trong Bài 1: Đường thẳng và mặt phẳng trong không gian Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 94.

Giải Toán 11 trang 94 Tập 1 Cánh diều

Bài 1 trang 94 Toán 11 Tập 1: Khi trát tường, dụng cụ không thể thiếu của người thợ là thước dẹt dài (Hình 28). Công dụng của thước dẹt này là gì? Giải thích.

Lời giải:

Công dụng của thước dẹt: Kiểm tra xem mặt tường đã phẳng chưa.

$\Rightarrow$ Áp thước vào mặt tường, nếu toàn bộ thước áp khít vào mặt tường thì mặt tường đã được trát phẳng, nếu thước không khít vào mặt tường thì cần bổ sung thêm vữa trát vào phần chưa khít đó.  

Bài 2 trang 94 Toán 11 Tập 1: Hình 29 là hình ảnh của chặn giấy gỗ có bốn mặt phân biệt là các tam giác. Vẽ hình biểu diễn của chặn giấy bằng gỗ đó.

Lời giải:

Hình biểu diễn của chặn giấy bằng gỗ là:

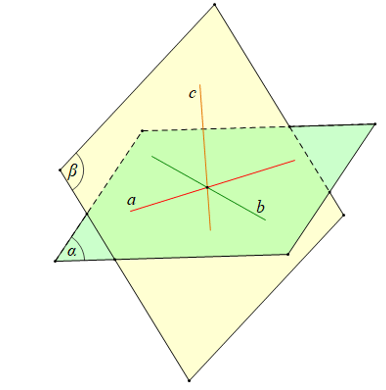
Bài 3 trang 94 Toán 11 Tập 1: Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.

Lời giải:

Giả sử a ∩ b = {I} và α = mp(a, b);

            a ∩ c = {J} và β = mp(a, c);

            b ∩ c = {K} và γ = mp(b, c) với các điểm I, J, K phân biệt.

Khi đó α ∩ β = a và đường thẳng a chính là đường thẳng IJ.

            α ∩ γ = b và đường thẳng b chính là đường thẳng IK.

            β ∩ γ = c và đường thẳng c chính là đường thẳng JK.

Mà chỉ có một mặt phẳng duy nhất đi qua ba điểm I, J, K, đó là (IJK)

Khi đó a, b, c cùng thuộc mặt phẳng (IJK), điều này trái với giả thiết a, b, c không cùng nằm trong một mặt phẳng.

Vậy I, J, K phải trùng nhau hay a, b, c đồng quy.

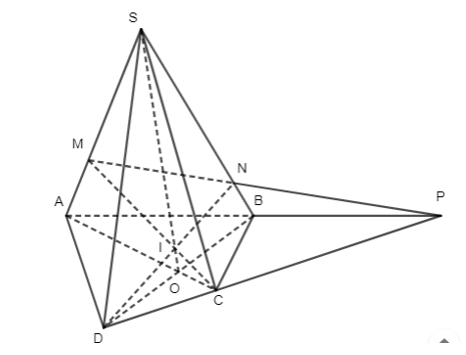
Bài 4 trang 94 Toán 11 Tập 1: Cho hình chóp S.ABCD có AC cắt BD tại O và AB cắt CD tại P. Điểm M thuộc cạnh SA (M khác S, M khác A). Gọi N là giao điểm của MP và SB, I là giao điểm của MC và DN. Chứng minh rằng S, O, I thẳng hàng.

Lời giải:

• Ta có: S ∈ (SAC) và S ∈ (SBD)

Do đó S là giao điểm của (SAC) và (SBD).

Mặt khác: AC ∩ BD = {O}.

                 AC ⊂ (SAC);

                 BD ⊂ (SBD).

Do đó O là giao điểm của (SAC) và (SBD).

Suy ra (SAC) ∩ (SBD) = SO.

• Trong mặt phẳng (DMNC) có:

   DN ∩ MC = {I}.

   DN ⊂ (SDB);

   MC ⊂ (SAB).

Do đó I là giao điểm của (SAC) và (SBD).

Suy ra giao tuyến SO của hai mặt phẳng này đi qua điểm I.

Hay I ∈ SO.

Vậy S, I, O thẳng hàng.

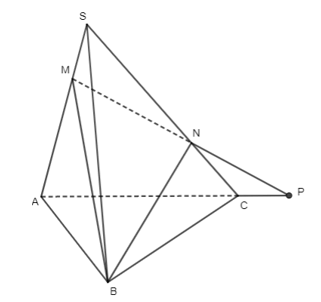
Bài 5 trang 94 Toán 11 Tập 1: Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho MA = 2MS, NS = 2NC.

a) Xác định giao điểm của MN với mặt phẳng (ABC).

b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC).

Lời giải:

a) Trong mặt phẳng (SAC), gọi giao điểm của MN và AC là P.

Mà AC ⊂ (SAC)

Do đó MN ∩ (ABC) = {P}.

b) Ta có MN ∩ (ABC) = {P} nên P ∈ (ABC)

Lại có P ∈ MN mà MN ⊂ (BMN) nên P ∈ (BMN)

Do đó P là giao điểm của (BMN) và (ABC).

Mặt khác: B ∈ (BMN) và B ∈ (ABC).

Do đó B là giao điểm của (BMN) và (ABC).

Vì vậy (BMN) ∩ (ABC) = BP.

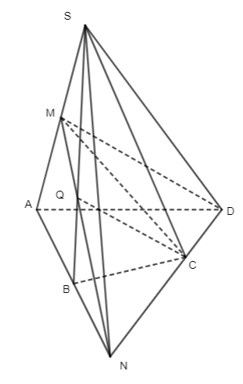
Bài 6 trang 94 Toán 11 Tập 1: Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.

a) Xác định giao điểm của CD với mặt phẳng (SAB).

b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).

c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC).

Lời giải:

a) Trong mặt phẳng (ABCD) ta có: gọi giao điểm của AB và CD là N.

Mà AB ⊂ (SAB)

Do đó CD ∩ (SAB) = {N}.

b) Ta có: AB ∩ CD = {N};

               AB ⊂ (SAB);

               CD ⊂ (SCD)

Do đó N là giao điểm của (SAB) và (SCD).

Lại có: S ∈ (SAB) và S ∈ (SCD).

Nên S là giao điểm của (SAB) và (SCD).

Vì vậy (SAB) ∩ (SCD) = SN.

c) Ta có: C ∈ (SBC) và C ∈ (MCD).

Do đó C là giao điểm của (SBC) và (MCD).

Trong mặt phẳng (SAB), gọi Q là giao điểm của MN và SB.

Mà MN ⊂ (MCD) và SB ⊂ (SBC)  

Suy ra Q là giao điểm của (SBC) và (MCD).

Vì vậy (SBC) ∩ (MCD) = CQ.

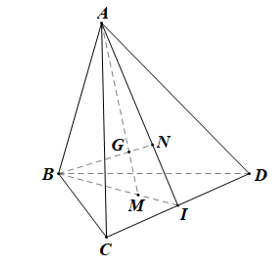
Bài 7 trang 94 Toán 11 Tập 1: Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA.

a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI).

b) Gọi G là giao điểm của AM và BN. Chứng minh rằng: $\frac{GM}{GA}=\frac{GN}{GB}=\frac{1}{3}$ .

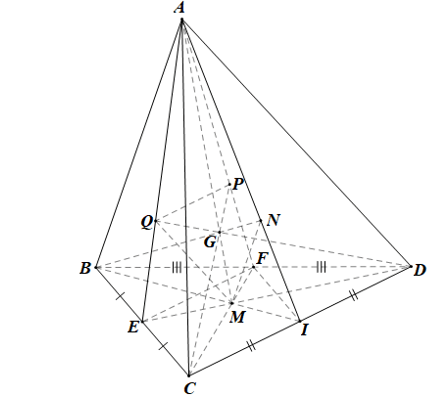
c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và $\frac{GP}{GC}=\frac{GQ}{GD}=\frac{1}{3}$ .

Lời giải:

a)

+) Xét tam giác BCD có: I là trung điểm của CD nên BI là đường trung tuyến.

Mà M là trọng tâm tam giác BCD nên BI đi qua M.

Do đó M ∈ BI.

Lại có AI ⊂ (ABI) nên M ∈ (ABI).

+) Xét tam giác ACD có: I là trung điểm của CD nên AI là đường trung tuyến.

Mà N là trọng tâm tam giác ACD nên AI đi qua N.

Do đó N ∈ AI.

Lại có BI ⊂ (ABI) nên N ∈ (ABI).

b) Trong $∆$BCD có M là trọng tâm tam giác nên $\frac{MI}{BI}=\frac{1}{3}$ .

Trong $∆$ACD có N là trọng tâm tam giác nên $\frac{NI}{AI}=\frac{1}{3}$ .

Xét $∆$ABI có: $\frac{NI}{AI}=\frac{MI}{BI}=\frac{1}{3}$  nên MN // AB (theo định lí Thalès đảo).

Xét $∆$ABI và MN // AB, theo hệ quả định lí Thalès ta có $\frac{MN}{AB}=\frac{NI}{AI}=\frac{MI}{BI}=\frac{1}{3}$ .

Xét $∆$ABG và MN // AB, theo hệ quả định lí Thalès ta có $\frac{GM}{GA}=\frac{GN}{GB}=\frac{MN}{AB}=\frac{1}{3}$ .

c)

• Gọi G’ là giao điểm của AM và CP; G’’ là giao điểm của AM và DQ.

Chứng minh tương tự câu b, ta có: $\frac{G^{\text{'}}M}{G^{\text{'}}A}=\frac{G^{\text{'}}P}{G^{\text{'}}C}=\frac{PM}{AC}=\frac{1}{3}$  và $\frac{{G^{\text{'}}}^{\text{'}}M}{{G^{\text{'}}}^{\text{'}}A}=\frac{{G^{\text{'}}}^{\text{'}}Q}{{G^{\text{'}}}^{\text{'}}D}=\frac{QM}{AD}=\frac{1}{3}$

Do đó $\frac{GM}{GA}=\frac{G^{\text{'}}M}{G^{\text{'}}A}=\frac{{G^{\text{'}}}^{\text{'}}M}{{G^{\text{'}}}^{\text{'}}A}=\frac{1}{3}$ .

Mà G, G’, G’’ cùng nằm trên AM nên G ≡ G’ ≡ G’’.

Vậy các đường thẳng CP, DQ cùng đi qua điểm G.

• Xét tam giác ABC, kẻ đường trung tuyến AE (E ∈ BC).

Ta có: Q là trọng tâm DABC nên $\frac{AQ}{AE}=\frac{2}{3}$.

Xét tam giác ABD, kẻ đường trung tuyến AF (F ∈ BD).

Ta có: P là trọng tâm $∆$ABD nên $\frac{AP}{AF}=\frac{2}{3}$.

+) Trong mặt phẳng (AEF), có: $\frac{AQ}{AE}=\frac{AP}{AF}=\frac{2}{3}$ nên PQ // EF (định lí Thalès đảo)

Mà EF // CD (đường trung bình tam giác BCD).

Suy ra PQ // CD

Theo hệ quả định lí Thalès ta có: $\frac{GP}{GC}=\frac{GQ}{GD}=\frac{QP}{CD}=\frac{QP}{2EF}=\frac{1}{2}.\frac{2}{3}=\frac{1}{3}$ .

Lời giải bài tập Toán 11 Bài 1: Đường thẳng và mặt phẳng trong không gian hay khác:

• Giải Toán 11 trang 86
• Giải Toán 11 trang 87
• Giải Toán 11 trang 89
• Giải Toán 11 trang 90
• Giải Toán 11 trang 92