Bài 11 trang 128 Toán 11 Tập 1 Chân trời sáng tạo
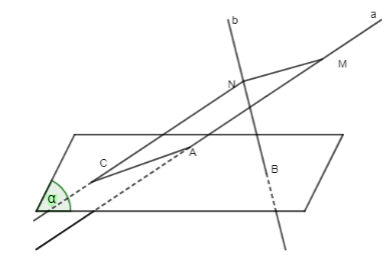
Cho mặt phẳng (α) và hai đường thẳng chéo nhau a, b cắt (α) tại A và B. Gọi d là đường thẳng thay đổi luôn luôn song song với (α) và cắt a tại M, cắt b tại N. Qua điểm N dựng đường thẳng song song với a cắt (α) tại điểm C.
Giải Toán 11 Bài tập cuối chương 4 - Chân trời sáng tạo
Bài 11 trang 128 Toán 11 Tập 1: Cho mặt phẳng (α) và hai đường thẳng chéo nhau a, b cắt (α) tại A và B. Gọi d là đường thẳng thay đổi luôn luôn song song với (α) và cắt a tại M, cắt b tại N. Qua điểm N dựng đường thẳng song song với a cắt (α) tại điểm C.
a) Tứ giác MNCA là hình gì?
b) Chứng minh rằng điểm C luôn luôn chạy trên một đường thẳng cố định.
c) Xác định vị trí của đường thẳng d để độ dài MN nhỏ nhất.
Lời giải:
a) Vì d // (α) nên phép chiếu song song của d trên mặt phẳng (α) là AC và d // AC hay MN // AC.
Mặt khác ta lại có AM // NC
Do đó tứ giác MNCA là hình bình hành.
b) C luôn chạy trên đường thẳng là hình chiếu của đường thẳng b trên mặt phẳng (α) theo phương chiếu (α).
d) Để độ dài MN nhỏ nhất thì đường thẳng d phải vuông góc với a và vuông góc với b.
Lời giải bài tập Toán 11 Bài tập cuối chương 4 hay, chi tiết khác:
Bài 3 trang 127 Toán 11 Tập 1: Cho hình chóp SABCD có AC cắt BD tại M, AB cắt CD tại N ....
Bài 6 trang 127 Toán 11 Tập 1: Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 10 ....