Bài 12 trang 128 Toán 11 Tập 1 Chân trời sáng tạo
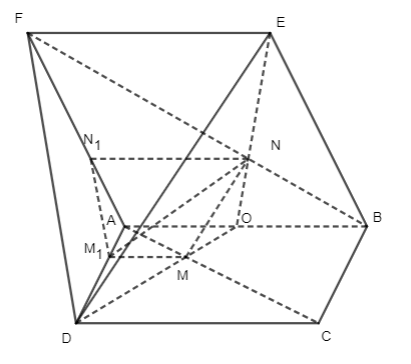
Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng hoàn toàn khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC và BF sao cho MC = 2MA; NF = 2NB. Qua M, N kẻ các đường thẳng song song với AB, cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:
Giải Toán 11 Bài tập cuối chương 4 - Chân trời sáng tạo
Bài 12 trang 128 Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng hoàn toàn khác nhau. Lấy các điểm M, N lần lượt thuộc các đường chéo AC và BF sao cho MC = 2MA; NF = 2NB. Qua M, N kẻ các đường thẳng song song với AB, cắt các cạnh AD, AF lần lượt tại M1, N1. Chứng minh rằng:
a) MN // DE;
b) M1N1 // (DEF);
c) (MNN1M1) // (DEF).
Lời giải:
+) Trong mặt phẳng (ABCD) kéo dài DM cắt AB tại O
Vì AO // DC nên (định lí Thales)
Suy ra .
+) Gọi N’ là giao điểm của BF và OE, khi đó: nên N’ trùng N.
+) Trong mặt phẳng (ODE), có: .
Suy ra MN // DE (định lí Thales đảo).
b) Ta có: MM1 // AB // DC nên .
Ta lại có: NN1 // AB // EF nên .
Suy ra
Do đó M1N1 // DF
Mà DF ⊂ (DEF) nên M1N1 // (DEF).
c) Ta có: MN // DE, M1N1 // DF mà DE, DF ⊂ (DEF) và MN, M1N1 ⊂ (MNN1M1); DE và DF cắt nhau tại E nên (MNN1M1) // (DEF).
Lời giải bài tập Toán 11 Bài tập cuối chương 4 hay, chi tiết khác:
Bài 3 trang 127 Toán 11 Tập 1: Cho hình chóp SABCD có AC cắt BD tại M, AB cắt CD tại N ....
Bài 6 trang 127 Toán 11 Tập 1: Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 10 ....