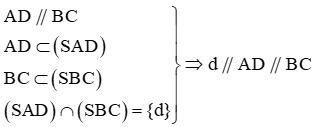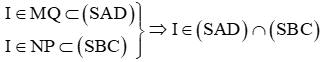Bài 3 trang 112 Toán 11 Tập 1 Chân trời sáng tạo
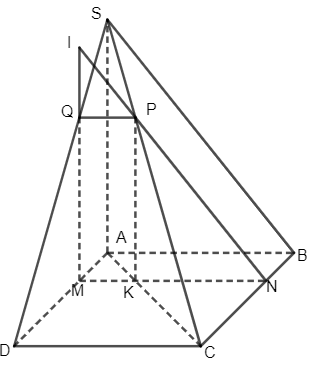
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M di động trên cạnh AD. Một mặt phẳng (α) qua M, song song với CD và SA, cắt BC, SC, SD lần lượt N, P, Q.
Giải Toán 11 Bài 3: Đường thẳng và mặt phẳng song song - Chân trời sáng tạo
Bài 3 trang 112 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và một điểm M di động trên cạnh AD. Một mặt phẳng (α) qua M, song song với CD và SA, cắt BC, SC, SD lần lượt N, P, Q.
a) MNPQ là hình gì?
b) Gọi I = MQ ∩ NP. Chứng minh rằng I luôn luôn thuộc một đường thẳng cố định khi M di động trên AD.
Lời giải:
a) Trong mặt phẳng (ABCD), từ M kẻ đường thẳng song song CD cắt BC tại N.
Gọi K là giao điểm của MN và AC.
Trong mặt phẳng (SAC), từ K kẻ đường thẳng song song với SA cắt SC tại P.
Trong mặt phẳng (SCD), từ P kẻ đường thẳng song song với CD cắt SD ở Q.
Mặt phẳng (MNPQ) chính là mặt phẳng (α) cần dựng.
b) Gọi d là giao tuyến của (SAD) ∩ (SBC)
Ta có:
Mà S ∈ (SAD) ∩ (SBC) nên S ∈ d
Ta lại có:
Do đó I ∈ d
Vì vậy I thuộc đường thẳng d cố định đi qua S và song song với AD.
Lời giải bài tập Toán 11 Bài 3: Đường thẳng và mặt phẳng song song hay, chi tiết khác: