Thực hành 7 trang 95 Toán 11 Tập 1 Chân trời sáng tạo

Cho hai đường thẳng a và b cắt nhau tại O và điểm M không thuộc mặt phẳng (a, b).

Giải Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian - Chân trời sáng tạo

Thực hành 7 trang 95 Toán 11 Tập 1: Cho hai đường thẳng a và b cắt nhau tại O và điểm M không thuộc mặt phẳng (a, b).

a) Tìm giao tuyến của hai mặt phẳng (M, a) và (M, b).

b) Lấy A, B lần lượt là hai điểm trên a, b và khác với điểm O. Tìm giao tuyến của (MAB) và mp(a, b).

c) Lấy điểm A’ trên đoạn MA và điểm B’ trên đoạn MB sao cho đường thẳng A’B’ cắt mp(a, b) tại C. Chứng minh ba điểm A, B, C thẳng hàng.

Lời giải:

a) Ta có hình vẽ sau:

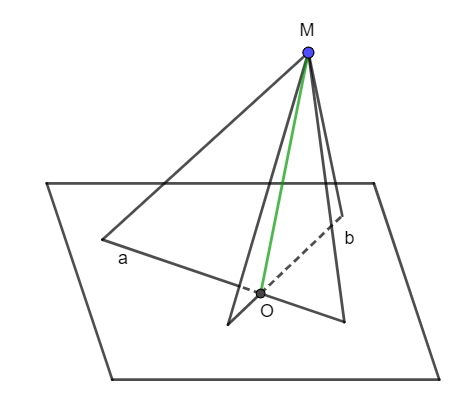
Thực hành 7 trang 95 Toán 11 Tập 1 Chân trời sáng tạo

Ta có:

M ∈ mp(M, a) và M ∈ mp(M, b) nên M ∈ (M, a) ∩ (M, b).

O là giao điểm của hai đường thẳng a và b, mà a ⊂ mp(M, a) và b ⊂ mp(M, b) nên O ∈ (M, a) ∩ (M, b).

Vậy giao tuyến của hai mặt phẳng (M, a) và (M, b) là đường thẳng qua hai điểm M và O.

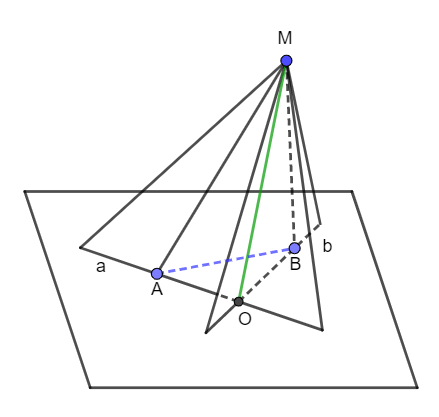
Thực hành 7 trang 95 Toán 11 Tập 1 Chân trời sáng tạo

Ta có: A ∈ (MAB) và A ∈ a ⊂ mp(a, b) nên A ∈ (MAB) ∩ mp(a, b).

Ta lại có: B ∈ (MAB) và B ∈ b ⊂ mp(a, b) nên B ∈ (MAB) ∩ mp(a, b).

Vậy giao tuyến của (MAB) và mp(a, b) là đường thẳng AB.

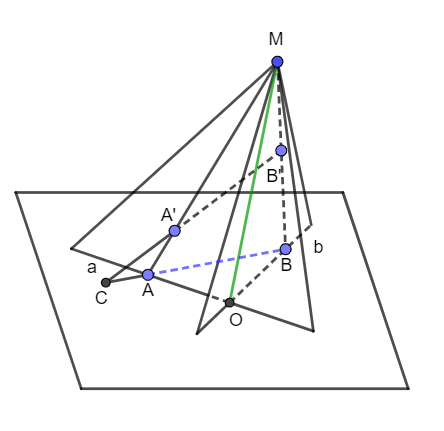
Thực hành 7 trang 95 Toán 11 Tập 1 Chân trời sáng tạo

Ta có (MA’B’) cũng là mặt phẳng (MAB)

Mà (MAB) giao mp(a, b) là đường thẳng AB nên điểm C cũng thuộc đường thẳng này do đó ba điểm A, B, C thẳng hàng.

Lời giải bài tập Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian hay, chi tiết khác: