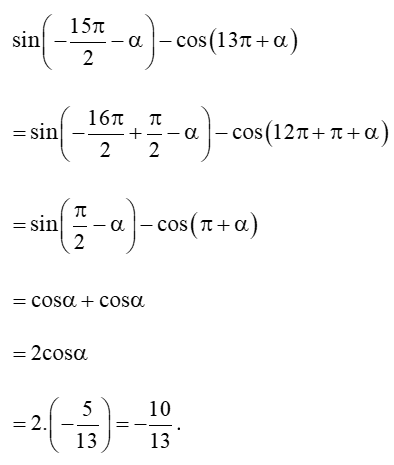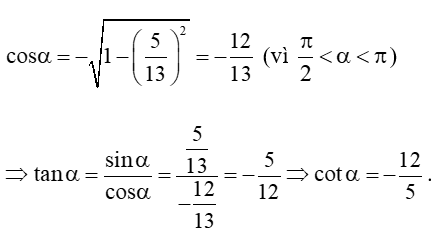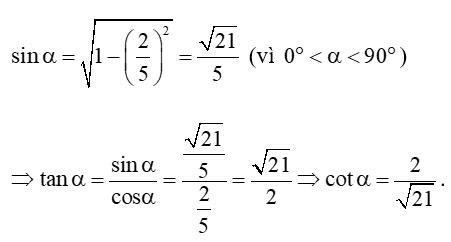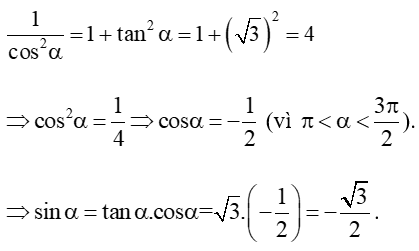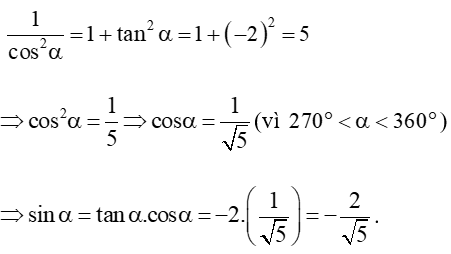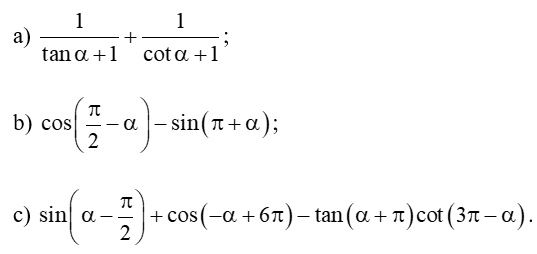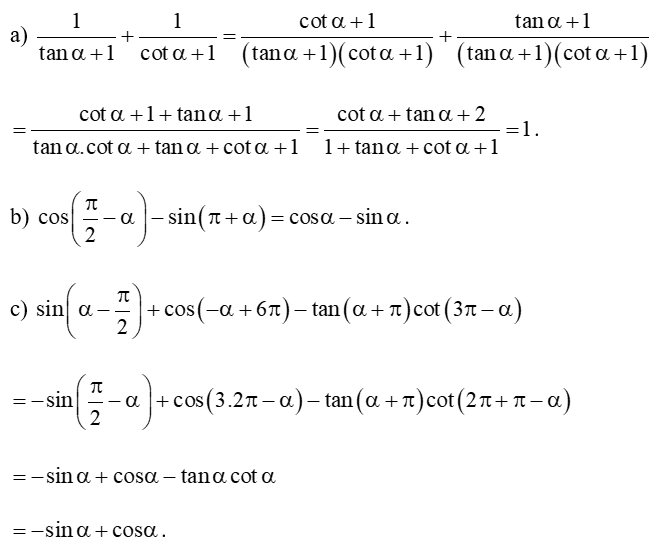Giải Toán 11 trang 19 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 19 Tập 1 trong Bài 2: Giá trị lượng giác của một góc lượng giác Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 19.

Giải Toán 11 trang 19 Tập 1 Chân trời sáng tạo

Thực hành 4 trang 19 Toán 11 Tập 1:

a) Biểu diễn cos638° qua giá trị lượng giác của góc có số đo từ 0° đến 45°.

b) Biểu diễn cot$\frac{19\pi }{5}$ qua giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$.

Lời giải:

a) Ta có: cos638° = cos(2.360° + (– 82°)) = cos(– 82°) = cos82° = cos(90° – 8°) = sin8°.

b) Ta có: $\cot \frac{19\pi }{5}=\cot \left(4\pi -\frac{\pi }{5}\right)=\cot \left(-\frac{\pi }{5}\right)=-\cot \frac{\pi }{5}$.

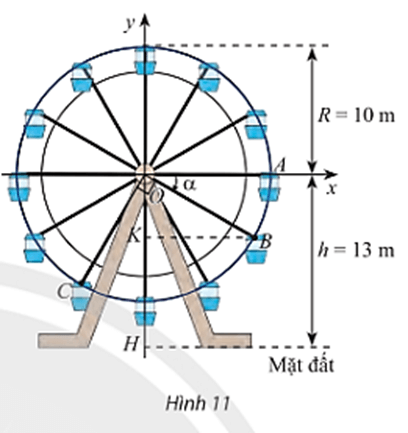
Vận dụng trang 19 Toán 11 Tập 1: Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu bởi điểm B và C.

a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng (13 + 10sinα) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi α = – 30°.

b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.

Lời giải:

a) Ta có điểm B là điểm biểu diễn cho góc lượng giác có số đo góc là α trên đường tròn lượng giác có bán kính bằng 10 nên tọa độ điểm B(10cosα; 10sinα).

Vì vậy chiều cao từ điểm B đến mặt đất là: 13 + 10sinα (mét).

Với α = – 30° ta có chiều cao từ điểm B đến mặt đất là: 13 + 10sin.(– 30°) = 8 (mét).

b) Đặt (OA, OC) = β = α – 90°

Nếu điểm B cách mặt đất 4m thì 13 + 10sinα = 4

⇔ sinα = $-\frac{9}{10}$

Ta có sinα = cos(α – 90°) = $-\frac{9}{10}$

⇒ cos(α – 90°) = $-\frac{9}{10}$

⇒ cosβ = $-\frac{9}{10}$

⇒ sinβ = $-\sqrt{1^2-{\left(\frac{9}{10}\right)}^2}=-\frac{\sqrt{19}}{10}$

Vì vậy chiều cao từ điểm C đến mặt đất là: 13 + 10sinβ = 13 + 10.$\left(-\frac{\sqrt{19}}{10}\right)$ ≈ 8,64 (mét).

Bài 1 trang 19 Toán 11 Tập 1: Các đẳng thức sau có thể đồng thời xảy ra không?

a) sinα = $\frac{3}{5}$ và cosα = $-\frac{4}{5}$;

b) sinα = $\frac{1}{3}$ và cotα = $\frac{1}{2}$;

c) tanα = 3 và cotα = $\frac{1}{3}$.

Lời giải:

a) Với – 1 ≤ sinα = $\frac{3}{5}$ ≤ 1 và – 1 ≤ cosα = $-\frac{4}{5}$ ≤ 1, ta có:

sin²α + cos²α = ${\left(\frac{3}{5}\right)}^2+{\left(-\frac{4}{5}\right)}^2$= 1.

Vậy sinα = $\frac{3}{5}$ và cosα = $-\frac{4}{5}$ có thể đồng thời xảy ra.

b) Với – 1 ≤ sinα = $\frac{1}{3}$ ≤ 1 và cotα = $\frac{1}{2}$, ta có:

1 + cot²α = $1+{\left(\frac{1}{2}\right)}^2=1+\frac{1}{4}=\frac{5}{4}$

$\frac{1}{{\sin }^2\alpha }=\frac{1}{{\left(\frac{1}{3}\right)}^2}=9$

Do đó 1 + cot²α ≠ $\frac{1}{{\sin }^2\alpha }$.

Vì vậy sinα = $\frac{1}{3}$ và cotα = $\frac{1}{2}$ không đồng thời xảy ra.

c) Với tanα = 3 và cotα = $\frac{1}{3}$, ta có:

tanα . cotα = 3. $\frac{1}{3}$ = 1.

Vì vậy tanα = 3 và cotα = $\frac{1}{3}$ đồng thời xảy ra.

Bài 2 trang 19 Toán 11 Tập 1: Cho sinα = $\frac{12}{13}$ và cosα = $-\frac{5}{13}$. Tính $\sin \left(-\frac{15\pi }{2}-\alpha \right)-\text{cos}\left(13\pi +\alpha \right)$.

Lời giải:

Bài 3 trang 19 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, nếu:

a) sin$\alpha$ = $\frac{5}{13}$ và $\frac{\pi }{2}<\alpha <\pi$;

b) cos$\alpha$ = $\frac{2}{5}$ và $0°<\alpha <90°$;

c) tan$\alpha$ = $\sqrt{3}$ và $\pi <\alpha <\frac{3\pi }{2}$;

d) cot$\alpha$ = $\frac{1}{2}$ và $270°<\alpha <360°$.

Lời giải:

a) Ta có:

Vậy $\text{cos}\alpha =-\frac{12}{13},\tan \alpha =-\frac{5}{12},\cot \alpha =-\frac{12}{5}$.

b) Ta có:

Vậy $\sin \alpha =\frac{\sqrt{21}}{5},\tan \alpha =\frac{\sqrt{21}}{2},\cot \alpha =\frac{2}{\sqrt{21}}$.

c) Ta có: tan$\alpha$ = $\sqrt{3}$$\Rightarrow$cot$\alpha$ = $\frac{1}{\sqrt{3}}$

Ta lại có:

Vậy $\sin \alpha =-\frac{\sqrt{3}}{2},\text{cos}\alpha =-\frac{1}{2},\cot \alpha =\frac{1}{\sqrt{3}}$.

d) Ta có: $\text{cot}\alpha =-\frac{1}{2}\Rightarrow \text{tan}\alpha =-2$

Ta lại có:

Vậy $\sin \alpha =-\frac{2}{\sqrt{5}},\text{cos}\alpha =\frac{1}{\sqrt{5}},\tan \alpha =-2$.

Bài 4 trang 19 Toán 11 Tập 1: Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$ hoặc từ 0 đến 45° và tính:

a) cos$\frac{21\pi }{6}$;

b) sin$\frac{129\pi }{4}$;

c) tan1 020°.

Lời giải:

a) Ta có: .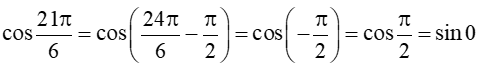

b) .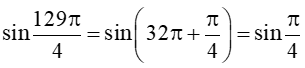

c) tan1 020° = tan(3.180° – 60°) = tan(180° – 60°) = – tan60° = – cot30°.

Bài 5 trang 19 Toán 11 Tập 1: Chứng minh đẳng thức lượng giác sau:

a) sin⁴α – cos⁴α = 1 – 2cos²α;

b) tanα + cotα = $\frac{1}{\sin \alpha .\text{cos}\alpha }$.

Lời giải:

a) Ta có: sin⁴α – cos⁴α = (sin²α – cos²α).(sin²α + cos²α ) = sin²α + cos²α – 2cos²α = 1 – 2cos²α.

b) Ta có: tanα + cotα =

.

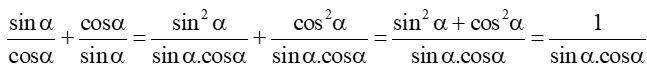
Bài 6 trang 19 Toán 11 Tập 1: Rút gọn các biểu thức sau:

Lời giải:

Lời giải bài tập Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 13

• Giải Toán 11 trang 15

• Giải Toán 11 trang 16

• Giải Toán 11 trang 17

• Giải Toán 11 trang 20