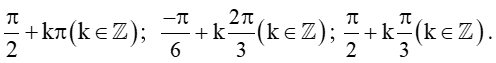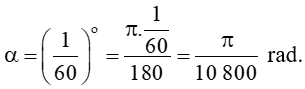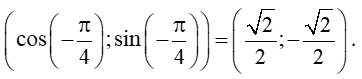Giải Toán 11 trang 13 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 13 Tập 1 trong Bài 1: Góc lượng giác Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 13.

Giải Toán 11 trang 13 Tập 1 Chân trời sáng tạo

Bài 7 trang 13 Toán 11 Tập 1: Trên đường tròn lượng giác hãy biểu diễn các góc lượng giác có số đo có dạng là:

a) $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$;

b) $k\frac{\pi }{4}\left(k\in \mathbb{Z}\right)$.

Lời giải:

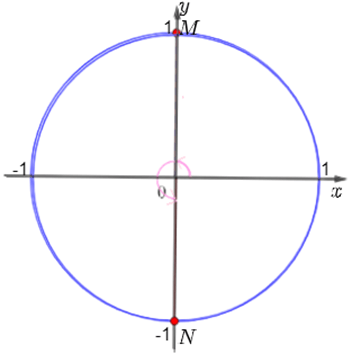
a) Với k = 0 thì có góc lượng giác có số đo góc là $\frac{\pi }{2}$, được biểu diễn bởi điểm M;

Với k = 1 thì có góc lượng giác có số đo góc là $\frac{\pi }{2}+\pi =\frac{3\pi }{2}$, được biểu diễn bởi điểm N;

Với k = 2 thì có góc lượng giác có số đo góc là $\frac{\pi }{2}+2\pi$ nên cũng được biểu diễn bởi điểm M;

Với k = 3 thì có góc lượng giác có số đo góc là $\frac{\pi }{2}+3\pi =\frac{3\pi }{2}+2\pi$ nên cũng được biểu diễn bởi điểm N.

Vậy với k chẵn thì các góc lượng giác có số đo dạng $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi điểm M, với k lẻ thì các góc lượng giác có số đo dạng $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi điểm N khi đó ta có hình vẽ sau:

b) Với k = 0 thì có góc lượng giác có số đo góc là 0, được biểu diễn bởi điểm A;

Với k = 1 thì có góc lượng giác có số đo góc là $\frac{\pi }{4}$, được biểu diễn bởi điểm M;

Với k = 2 thì có góc lượng giác có số đo góc là $\frac{2\pi }{4}=\frac{\pi }{2}$ được biểu diễn bởi điểm B;

Với k = 3 thì có góc lượng giác có số đo góc là $\frac{3\pi }{4}$ được biểu diễn bởi điểm N;

Với k = 4 thì có góc lượng giác có số đo góc là $\frac{4\pi }{4}=\pi$ được biểu diễn bởi điểm A’;

Với k = 5 thì có góc lượng giác có số đo góc là $\frac{5\pi }{4}$ được biểu diễn bởi điểm M’;

Với k = 6 thì có góc lượng giác có số đo góc là $\frac{6\pi }{4}=\frac{3\pi }{2}$ được biểu diễn bởi điểm B’;

Với k = 7 thì có góc lượng giác có số đo góc là $\frac{7\pi }{4}$ được biểu diễn bởi điểm N’;

Với k = 8 thì có góc lượng giác có số đo góc là $\frac{8\pi }{4}=2\pi +0$ nên được biểu diễn bởi điểm A;

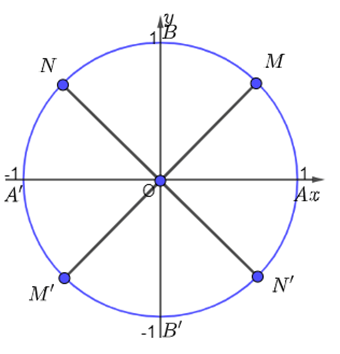
Vậy các góc lượng giác có số đo dạng $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi các điểm A, M, B, N, A’, M’, B’, N’. Khi đó ta có hình vẽ sau:

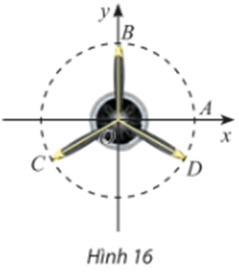
Bài 8 trang 13 Toán 11 Tập 1: Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể biểu diễn cho các góc lượng giác nào sau đây?

Lời giải:

+) Xét các góc lượng giác có số đo $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$

Với k chẵn ta có các góc lượng giác có số đo $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi điểm B;

Với k lẻ ta có các góc lượng giác có số đo $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ được biểu diễn bởi điểm B’(0; – 1).

Vì vậy các điểm B, C, D không thể biểu diễn cho các góc lượng giác có số đo $\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$.

+) Xét các góc lượng giác có số đo $\frac{-\pi }{6}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$

Với k = 0 ta có góc lượng giác có số đo $\frac{-\pi }{6}$ được biểu diễn bởi điểm D.

Với k = 1 ta có góc lượng giác có số đo $\frac{-\pi }{6}+\frac{2\pi }{3}=\frac{\pi }{2}$ được biểu diễn bởi điểm B.

Với k = 2 ta có góc lượng giác có số đo $\frac{-\pi }{6}+2.\frac{2\pi }{3}=\frac{7\pi }{6}$ được biểu diễn bởi điểm C.

Với k = 3 ta có góc lượng giác có số đo $\frac{-\pi }{6}+3.\frac{2\pi }{3}=\frac{-\pi }{6}+2\pi$ được biểu diễn bởi điểm D.

Vì vậy các góc lượng giác có số đo $\frac{-\pi }{6}+k\frac{2\pi }{3}\left(k\in \mathbb{Z}\right)$ được biểu diễn bởi các điểm B, C, D.

+) Xét các góc lượng giác có số đo $\frac{\pi }{2}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right)$

Với k = 0 ta có góc lượng giác có số đo $\frac{\pi }{2}$ được biểu diễn bởi điểm B.

Với k = 1 ta có góc lượng giác có số đo $\frac{\pi }{2}+\frac{\pi }{3}=\frac{5\pi }{6}$ được biểu diễn bởi điểm M.

Với k = 2 ta có góc lượng giác có số đo $\frac{\pi }{2}+2\frac{\pi }{3}=\frac{7\pi }{6}$ được biểu diễn bởi điểm C.

Với k = 3 ta có góc lượng giác có số đo $\frac{\pi }{2}+3\frac{\pi }{3}=\frac{3\pi }{2}$ được biểu diễn bởi điểm B’.

Với k = 4 ta có góc lượng giác có số đo $\frac{\pi }{2}+4\frac{\pi }{3}=\frac{11\pi }{6}=-\frac{\pi }{6}+2\pi$ được biểu diễn bởi điểm D.

Với k = 5 ta có góc lượng giác có số đo $\frac{\pi }{2}+5\frac{\pi }{3}=\frac{13\pi }{6}=\frac{\pi }{6}+2\pi$ được biểu diễn bởi điểm N.

Với k = 6 ta có góc lượng giác có số đo $\frac{\pi }{2}+6\frac{\pi }{3}=\frac{\pi }{2}+2\pi$ được biểu diễn bởi điểm B.

Ví vậy các điểm B, C, D không thể biểu diễn cho các góc lượng giác có số đo là $\frac{\pi }{2}+k\frac{\pi }{3}\left(k\in \mathbb{Z}\right)$.

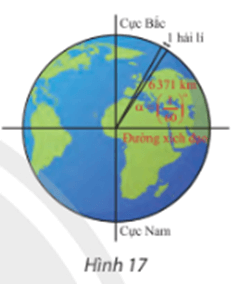
Bài 9 trang 13 Toán 11 Tập 1: Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc $\alpha ={\left(\frac{1}{60}\right)}^o$ của đường kinh tuyến (Hình 17). Đổi số đo α sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu ki lô mét, biết bán kính trung bình của Trái Đất là 6 371 km. Làm tròn kết quả hàng phần trăm.

Lời giải:

Ta có:

Độ dài cung chắn góc α là: α.R = $\frac{\pi }{10800}$.6 371 $\approx$ 1,85 km.

Vậy 1 hải lí bằng 1,85 km.

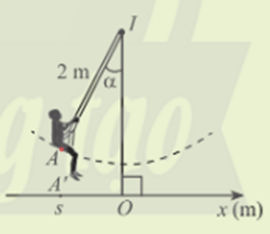
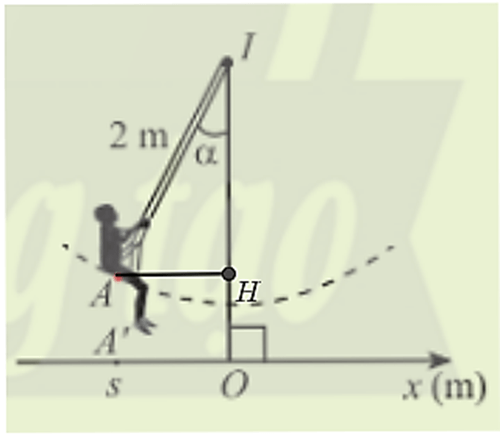
Hoạt động khởi động trang 13 Toán 11 Tập 1: Hình bên biểu diễn xích đu IA có độ dài 2m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A’ là hình chiếu của A lên Ox. Tọa độ s của A’ trên trục Ox được gọi là li độ của A và (IO, IA) = α được gọi là li độ góc của A. Làm cách nào để tính li độ dựa vào li độ góc?

Lời giải:

Kẻ AH vuông góc với IO tại H

Xét tam giác AHI vuông tại H, có:

AH = sinα . IA = 2sinα (m).

AH cũng chính là li độ của A nên s = 2sinα.

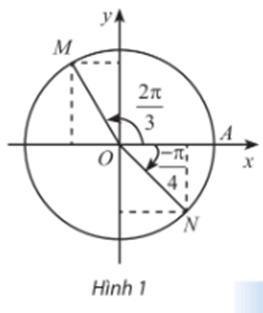
Hoạt động khám phá 1 trang 13 Toán 11 Tập 1: Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác $\frac{2\pi }{3}$ và $-\frac{\pi }{4}$ trên đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy.

Lời giải:

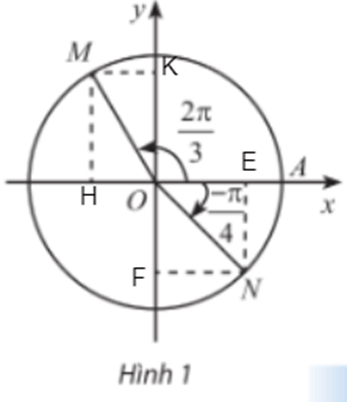
Gọi H, K lần lượt là hình chiếu của điểm M xuống trục Ox và Oy; gọi E, F lần lượt là hình chiếu của điểm N trên trục Ox và Oy.

Đặt (OA, OM) = $\alpha$, (OA, ON) = $\beta$.

+) Xét tam giác MHO vuông tại H, có:

MH = sin$\widehat{MOH}$.MO = sin$\widehat{MOH}$

Ta có $\widehat{MOH}+\widehat{AOM}=180°$ nên sin$\widehat{MOH}$ = sin$\widehat{AOM}$.

⇒ MH = sin$\widehat{AOM}$ = sinα.

Mà MH = OK nên OK = sinα hay tung độ điểm M bằng sinα.

Ta lại có: OH = cos$\widehat{MOH}$.MO = cos$\widehat{MOH}$

Mà $\widehat{MOH}+\widehat{AOM}=180°$ nên cos$\widehat{MOH}$ = -cos$\widehat{AOM}$

⇒ OH = -cos$\widehat{AOM}$ = – cosα do đó hoành độ của điểm M bằng cosα.

Vậy tọa độ điểm M là (cosα; sinα) = $\left(\text{cos}\frac{2\pi }{3};\sin \frac{2\pi }{3}\right)=\left(-\frac{1}{2};\frac{\sqrt{3}}{2}\right)$.

+) Xét tam giác ONE vuông tại E, có:

NE = sin$\widehat{NOE}$.ON = sin$\widehat{NOE}$

Mà $\widehat{NOE}$= -$\beta$

⇒ NE = – sinβ.

Mà NE = OF nên OF = – sinβ do đó tung độ điểm N bằng sinβ.

Ta lại có: OE = cos$\widehat{NOE}$.ON = cos$\widehat{NOE}$

⇒ OE = cosβ nên hoành độ của điểm M bằng cosβ.

Vậy tọa độ điểm N là

(cosβ; sinβ) =

Lời giải bài tập Toán 11 Bài 1: Góc lượng giác Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 7

• Giải Toán 11 trang 9

• Giải Toán 11 trang 10

• Giải Toán 11 trang 11

• Giải Toán 11 trang 12