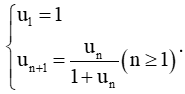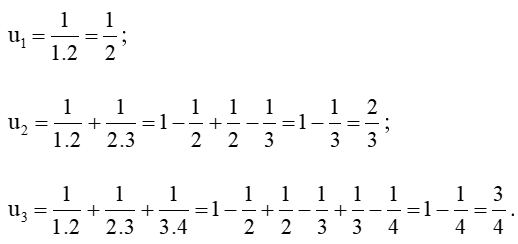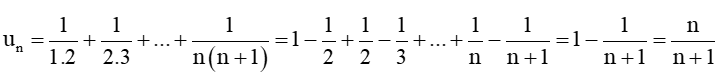Giải Toán 11 trang 50 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 50 Tập 1 trong Bài 1: Dãy số Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 50.

Giải Toán 11 trang 50 Tập 1 Chân trời sáng tạo

Bài 1 trang 50 Toán 11 Tập 1: Tìm u₂, u₃ và dự đoán công thức số hạng tổng quát của u_n dãy số:

Lời giải:

Ta có: n = 2 ≥ 1 nên $u_2=\frac{u_1}{1+u_1}=\frac{1}{1+1}=\frac{1}{2}$.

n = 3 ≥ 1 nên $u_3=\frac{u_2}{1+u_2}=\frac{\frac{1}{2}}{1+\frac{1}{2}}=\frac{1}{3}$.

n = 4 ≥ 1 nên $u_4=\frac{u_3}{1+u_3}=\frac{\frac{1}{3}}{1+\frac{1}{3}}=\frac{1}{4}$.

n = 5 ≥ 1 nên $u_5=\frac{u_4}{1+u_4}=\frac{\frac{1}{4}}{1+\frac{1}{4}}=\frac{1}{5}$.

Dự đoán công thức số hạng tổng quát u_n của dãy số là: $u_n=\frac{1}{n},\forall n\in {\mathbb{N}}^{*}$.

Bài 2 trang 50 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{1}{1.2}+\frac{1}{2.3}+\mathrm{...}+\frac{1}{n\left(n+1\right)}$. Tìm u₁, u₂, u₃ và dự đoán công thức số hạng tổng quát của u_n.

Lời giải:

Ta có:

Dự đoán công thức tổng quát:

Bài 3 trang 50 Toán 11 Tập 1: Xét tính tăng, giảm của dãy số (y_n) với $y_n=\sqrt{n+1}-\sqrt{n}$.

Lời giải:

Ta có: $y_{n+1}=\sqrt{\left(n+1\right)+1}-\sqrt{n+1}=\sqrt{n+2}-\sqrt{n+1}$.

Xét hiệu $y_{n+1}-y_n=\sqrt{n+2}-\sqrt{n+1}-\sqrt{n+1}+\sqrt{n}=\sqrt{n+2}+\sqrt{n}>0,\forall n\in {\mathbb{N}}^{*}$.

Suy ra y_n+1 > y_n, ∀n ∈ ℕ^*.

Vậy dãy số (y_n) tăng.

Bài 4 trang 50 Toán 11 Tập 1: Xét tính bị chặn của các dãy số sau:

a) (a_n) với $a_n={\sin }^2\frac{n\pi }{3}+\text{co}s\frac{n\pi }{4}$;

b) (u_n) với $u_n=\frac{6n-4}{n+2}$.

Lời giải:

a) Vì $0\le {\sin }^2\frac{n\pi }{3}\le 1,\forall n\in {\mathbb{N}}^{*}$ và $-1\le \cos \frac{n\pi }{4}\le 1,\forall n\in {\mathbb{N}}^{*}$ nên $-1\le {\sin }^2\frac{n\pi }{3}+\text{co}s\frac{n\pi }{4}\le 2,\forall n\in {\mathbb{N}}^{*}$

Do đó $-1\le a_n\le 2,\forall n\in {\mathbb{N}}^{*}$

Suy ra dãy số (a_n) bị chặn.

b) Ta có: $u_n=\frac{6n-4}{n+2}=6-\frac{16}{n+2}$

Vì n ∈ ℕ^* nên n ≥ 1 do đó ta có: n + 2 ≥ 3

$\Rightarrow -\frac{16}{n+2}\ge -\frac{16}{3}$

$\Rightarrow 6-\frac{16}{n+2}\ge 6-\frac{16}{3}$

$\Rightarrow u_n\ge \frac{2}{3}$.

Mặt khác n ∈ ℕ^* nên n > 0 do đó $\frac{16}{n+2}>0$ khi đó u_n < 6.

Suy ra $\frac{2}{3}\le u_n<6$ nên dãy số bị chặn trên và chặn dưới.

Vì vậy dãy số (u_n) bị chặn.

Bài 5 trang 50 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{2n-1}{n+1}$. Chứng minh (u_n) là dãy số tăng và bị chặn.

Lời giải:

Ta có: $u_n=\frac{2n-1}{n+1}=2-\frac{3}{n+1}$

Vì n ∈ ℕ^* nên n ≥ 1 do đó ta có: n + 1 ≥ 2

$\Rightarrow -\frac{3}{n+1}\ge -\frac{3}{2}$

$\Rightarrow 2-\frac{3}{n+1}\ge 2-\frac{3}{2}$

$\Rightarrow u_n\ge \frac{1}{2}$

Mặt khác n ∈ ℕ^* nên n > 0 do đó $\frac{3}{n+1}>0$ khi đó u_n < 2.

Suy ra $\frac{1}{3}\le u_n<2$ nên dãy số bị chặn trên và chặn dưới.

Vì vậy dãy số (u_n) bị chặn.

Ta có: $u_{n+1}=\frac{2\left(n+1\right)-1}{n+1+1}=\frac{2n+1}{n+2}$

Xét hiệu:

$u_{n+1}-u_n=\frac{2n+1}{n+2}-\frac{2n-1}{n+1}=\frac{2n^2+3n+1-2n^2-3n+2}{(n+1)(n+2)}=\frac{3}{(n+1)(n+2)}>0,\forall n\in {\mathbb{N}}^{*}$.

Suy ra u_n+1 > u_n nên dãy số (u_n) tăng.

Vậy dãy số (u_n) tăng và bị chặn.

Bài 6 trang 50 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{na+2}{n+1}$. Tìm các giá trị của a để:

a) (u_n) là dãy số tăng;

b) (u_n) là dãy số giảm.

Lời giải:

Ta có: $u_{n+1}=\frac{\left(n+1\right)a+2}{n+1+1}=\frac{\left(n+1\right)a+2}{n+2}$

Xét hiệu:

$u_{n+1}-u_n=\frac{\left(n+1\right)a+2}{n+2}-\frac{na+2}{n+1}=\frac{\left(\left(n+1\right)a+2\right)\left(n+1\right)}{\left(n+2\right)\left(n+1\right)}-\frac{\left(na+2\right)\left(n+2\right)}{\left(n+1\right)\left(n+2\right)}$

$=\frac{\left(n^2+2n+1\right)a+2n+2}{\left(n+2\right)\left(n+1\right)}-\frac{\left(n^2+2n\right)a+2n+4}{\left(n+1\right)\left(n+2\right)}=\frac{a-2}{\left(n+1\right)\left(n+2\right)}$

Vì n ∈ ℕ^* nên (n + 1)(n + 2) > 0 nên dấu của hiệu u_n+1 – u_n phụ thuộc vào dấu của biểu thức a – 2.

a) Để (u_n) là dãy số tăng thì u_n+1 – u_n > 0 nên a – 2 > 0 ⇔ a > 2.

b) Để (u_n) là dãy số giảm thì u_n+1 – u_n < 0 nên a – 2 < 0 ⇔ a < 2.

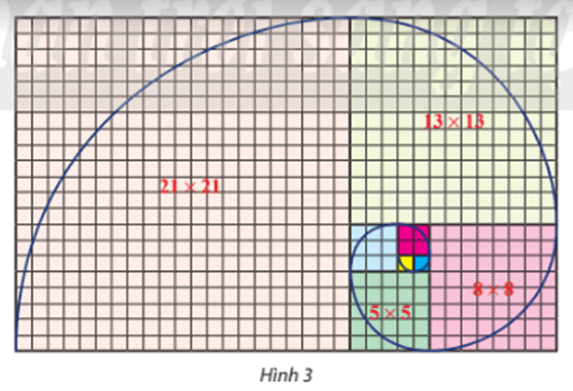
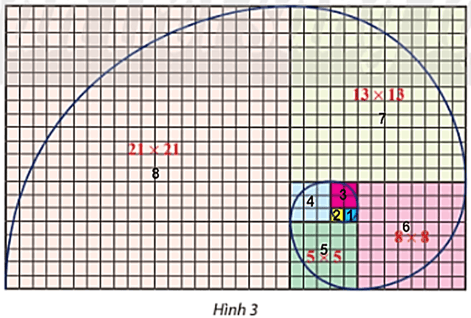
Bài 7 trang 50 Toán 11 Tập 1: Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đó từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?

Lời giải:

Độ dài cạnh của hình vuông số 1 là: 1;

Độ dài cạnh của hình vuông số 2 là: 1;

Độ dài cạnh của hình vuông số 3 là: 2;

Độ dài cạnh của hình vuông số 4 là: 3;

Độ dài cạnh của hình vuông số 5 là: 5;

Độ dài cạnh của hình vuông số 6 là: 8;

Độ dài cạnh của hình vuông số 7 là: 13;

Độ dài cạnh của hình vuông số 8 là: 21.

Ta có dãy số: 1; 1; 2; 3; 5; 8; 13; 21.

Nhận xét: Dãy số trên có đặc điểm là:

Trong ba số hạng liên tiếp, số hạng thứ ba bằng tổng hai số hạng đầu.

Lời giải bài tập Toán 11 Bài 1: Dãy số Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 45

• Giải Toán 11 trang 46

• Giải Toán 11 trang 47

• Giải Toán 11 trang 48

• Giải Toán 11 trang 49