Giải Toán 11 trang 72 Tập 2 Chân trời sáng tạo

---

Với Giải Toán 11 trang 72 Tập 2 trong Bài 3: Hai mặt phẳng vuông góc Toán lớp 11 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 72.

Giải Toán 11 trang 72 Tập 2 Chân trời sáng tạo

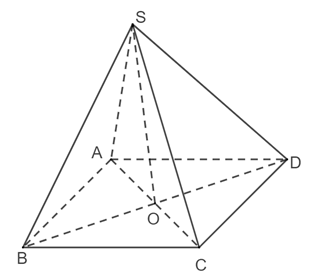
Thực hành 4 trang 72 Toán 11 Tập 2: Cho hình chóp tứ giác đều S.ABCD có O là tâm của đáy và AB = a, SA = 2a. Tính SO theo a.

Lời giải:

Vì S.ABCD là hình chóp tứ giác đều ⇒ SO ⊥ (ABCD)

⇒ SO ⊥ OA.

Ta có: ABCD là hình vuông $\Rightarrow \text{AC}=\sqrt{2{\mathrm{AB}}^2}=a\sqrt{2}\Rightarrow \text{AO}=\frac{1}{2}\mathrm{AC}=\frac{a\sqrt{2}}{2}$

Xét tam giác SOA vuông tại O:

$\mathrm{SO}=\sqrt{{\mathrm{SA}}^2-{\mathrm{AO}}^2}=\frac{a\sqrt{14}}{2}$ (theo định lí Pytago)

Vậy $\mathrm{SO}=\frac{a\sqrt{14}}{2}$

Vận dụng 4 trang 72 Toán 11 Tập 2: Cho biết kim tự tháp Khafre tại Ai Cập có dạng hình chóp tứ giác đều với chiều cao khoảng 136m và cạnh đáy dài khoảng 152m. Tính độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp.

(nguồn:https://vi.wikipedia.org/wiki/ Kim_tự_tháp_Khafre)

Lời giải:

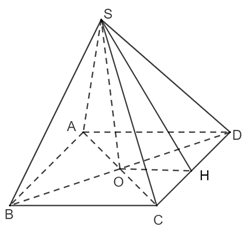
Mô hình hoá hình ảnh kim tự tháp bằng hình chóp tứ giác đều S.ABCD có O là tâm của đáy.

Kẻ SH ⊥ CD (H ∈ CD)

Ta có: SO = 136m , AD = 152 m

Tam giác SCD cân tại S

⇒ SH vừa là trung tuyến, vừa là đường cao của tam giác SCD

⇒ H là trung điểm của CD.

Mà O là trung điểm của AD.

⇒ OH là đường trung bình của tam giác ACD

⇒ $\mathrm{OH}=\frac{1}{2}\mathrm{AD}=76\left(m\right)$

Ta có: SO ⊥ (ABCD) SO ⊥ OH

⇒ ΔSOH vuông tại O.

⇒ $\mathrm{SH}=\sqrt{{\mathrm{SO}}^2+{\mathrm{OH}}^2}=\sqrt{{136}^2+{76}^2}\approx 155,8\left(m\right)$

Vậy độ dài đường cao của mặt bên xuất phát từ đỉnh của kim tự tháp khoảng 155,8 m.

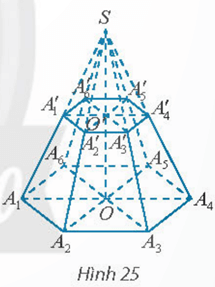
Hoạt động khám phá 8 trang 72 Toán 11 Tập 2: Cho hình chóp đều S.A₁A₂...A₆. Mặt phẳng (P) song song với mặt đáy và cắt các cạnh bên lần lượt tại A′₁A′₂...A′₆.

a) Đa giác A′₁A′₂...A′₆ có phái lục giác đều không? Giải thích.

b) Gọi O và O′ lần lượt là tâm của hai lục giác A₁A₂...A₆ và A′₁A′₂...A′₆. Đường thẳng OO′ có vuông góc với mặt đáy không?

Lời giải:

a) Ta có:(P) // (A₁A₂A₃...A₆)

Do đó A₁′A₂′ // A₁A₂; A₂′A₃′ // A₂A₃; A₃′A₄′ // A₃A₄;

A4′A5′ // A₄A₅; A₅′A₆′ // A₅A₆; A₆′A₁′ // A₆A₁

Khi đó $\frac{{A^{\text{'}}}_1{A^{\text{'}}}_2}{A_1{A}_2}=\frac{{A^{\text{'}}}_2{A^{\text{'}}}_3}{A_2{A}_3}=\frac{{A^{\text{'}}}_3{A^{\text{'}}}_4}{A_3{A}_4}=\frac{{A^{\text{'}}}_4{A^{\text{'}}}_5}{A_4{A}_5}=\frac{{A^{\text{'}}}_5{A^{\text{'}}}_6}{A_5{A}_6}=\frac{{A^{\text{'}}}_6{A^{\text{'}}}_1}{A_6{A}_1}$.

Mà A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅ = A₅A₆ = A₆A₁

⇒ A₁′A₂′ = A₂′A₃′ = A₃′A₄′ = A₄′A₅′ = A₅′A₆′ = A₆′A₁′

Vậy đa giác A′₁A′₂...A′₆ là lục giác đều.

b) Ta có:

$\left.\begin{array}{c}\mathrm{O}\text{'}\in {{\mathrm{A}}^{\text{'}}}_1{{\mathrm{A}}^{\text{'}}}_4\subset \left(\text{S}{\mathrm{A}}_1{\mathrm{A}}_4\right)\\ \mathrm{O}\text{'}\in {{\mathrm{A}}^{\text{'}}}_3{{\mathrm{A}}^{\text{'}}}_6\subset \left({\mathrm{SA}}_3{\mathrm{A}}_6\right)\\ \left(\text{S}{\mathrm{A}}_1{\mathrm{A}}_4\right)\cap \left({\mathrm{SA}}_3{\mathrm{A}}_6\right)=\mathrm{SO}\end{array}\right\}\Rightarrow {\mathrm{O}}^{\text{'}}\in \mathrm{SO}$

Mà S.A₁A₂...A₆ là hình chóp đều nên SO ⊥ (A₁A₂...A₆ ).

Vậy OO′ ⊥ (A₁A₂...A₆).

Lời giải bài tập Toán 11 Bài 3: Hai mặt phẳng vuông góc hay khác:

• Giải Toán 11 trang 65

• Giải Toán 11 trang 67

• Giải Toán 11 trang 69

• Giải Toán 11 trang 71

• Giải Toán 11 trang 73

• Giải Toán 11 trang 74