a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, giải thích vì sao MK  MH (H.7.74).

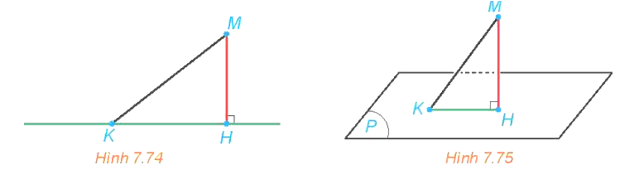
b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M lên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ³ MH (H7.75).

Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).

a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').

b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.

Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M; N bất kỳ thuộc a và gọi A; B tương ứng là các hình chiếu của chúng trên (P) (H.7.78).

Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).