Câu hỏi:
b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.
Trả lời:
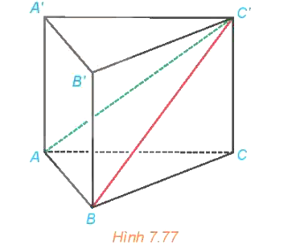
b) Vì tam giác ABC vuông cân tại A nên AB ^ AC.
Vì AA' ^ (ABC) nên AA' ^ AB mà AB ^ AC nên AB ^ (ACC'A'), suy ra AB ^ AC'.
Do đó tam giác ABC' là tam giác vuông tại A.
Hạ AK ^ BC' tại K. Khi đó d(A, BC') = AK.
Vì ACC'A' là hình chữ nhật nên .
Xét tam giác ABC' vuông tại A, AK là đường cao, ta có:
.
Vậy khoảng cách từ A đến BC' bằng .
Câu 1:
a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, giải thích vì sao MK ³ MH (H.7.74).
Câu 2:
b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M lên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ³ MH (H7.75).
Câu 3:
Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).
a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').
Câu 4:
Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M; N bất kỳ thuộc a và gọi A; B tương ứng là các hình chiếu của chúng trên (P) (H.7.78).
Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).
Câu 5:
a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không?
b) Cho hai mặt phẳng song song (P) và (Q) và một điểm M thay đổi trên (P) (H.7.79). Hỏi khoảng cách từ M đến (Q) thay đổi thế nào khi M thay đổi.
Câu 6:
Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) thì giữa d(a, (Q)) và d((P), (Q)) có mối quan hệ gì?
Câu 7:
Cho hình chóp S.ABC có SA ^ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) Tính d((MNP), (ABC)) và d(NP, (ABC)).
