Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M; N bất kỳ thuộc a và gọi A; B tương ứng là các hình chiếu của chúng trên (P) (H.7.78). Giải thích vì sao ABNM là một hình chữ nh
Câu hỏi:
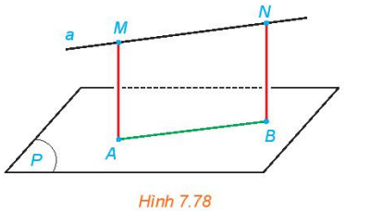
Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M; N bất kỳ thuộc a và gọi A; B tương ứng là các hình chiếu của chúng trên (P) (H.7.78).
Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).
Trả lời:
Vì A, B lần lượt là các hình chiếu của M, N trên (P) nên AM ^ (P), BN ^ (P).
Do đó AM // BN hay A, B, M, N cùng thuộc một mặt phẳng.
Vì MN // (P) và (ABNM) Ç (P) = AB nên MN // AB.
Vì AM // BN và MN // AB nên ABNM là hình bình hành.
Mặt khác AM ^ (P) nên AM ^ AB. Do đó ABNM là hình chữ nhật.
Vì ABNM là hình chữ nhật nên AM = BN nên M, N có cùng khoảng cách đến (P).