Bài 4.3 trang 77 Toán 11 Tập 1 - Kết nối tri thức
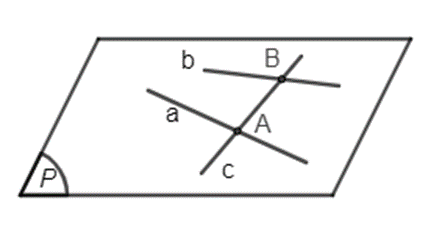
Cho mặt phẳng (P) và hai đường thẳng a, b nằm trong (P). Một đường thẳng c cắt hai đường thẳng a và b tại hai điểm phân biệt. Chứng minh rằng đường thẳng c nằm trong mặt phẳng (P).
Giải Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian - Kết nối tri thức
Bài 4.3 trang 77 Toán 11 Tập 1: Cho mặt phẳng (P) và hai đường thẳng a, b nằm trong (P). Một đường thẳng c cắt hai đường thẳng a và b tại hai điểm phân biệt. Chứng minh rằng đường thẳng c nằm trong mặt phẳng (P).
Lời giải:
Giả sử đường thẳng c cắt hai đường thẳng a và b lần lượt tại hai điểm phân biệt A và B.
Vì A thuộc a và a nằm trong (P) nên A thuộc (P).
Vì B thuộc B và b nằm trong (P) nên B thuộc (P).
Đường thẳng c có hai điểm phân biệt A và B cùng thuộc mặt phẳng (P) nên tất cả các điểm của đường thẳng c đều thuộc (P) hay đường thẳng c nằm trong mặt phẳng (P).
Lời giải bài tập Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian hay, chi tiết khác:
Câu hỏi trang 71 Toán 11 Tập 1: Hãy tìm một số hình ảnh của mặt phẳng trong thực tế. ....
Câu hỏi trang 72 Toán 11 Tập 1: Có bao nhiêu mặt phẳng đi qua ba điểm thẳng hàng? ....