Bài 4.32 trang 100 Toán 11 Tập 1 - Kết nối tri thức
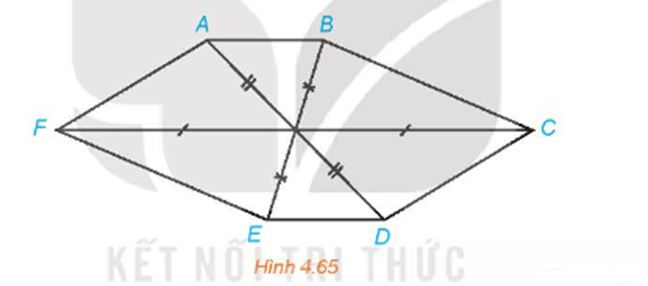
Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?
Giải Toán 11 Bài 14: Phép chiếu song song - Kết nối tri thức
Bài 4.32 trang 100 Toán 11 Tập 1: Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?
Lời giải:
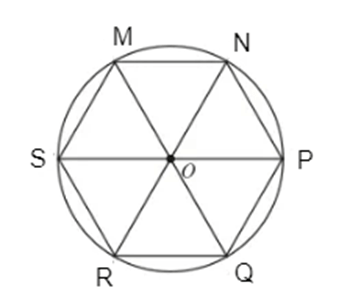
+) Xét hình lục giác đều MNPQRS có tâm O.
Ta nhận thấy:
- Tứ giác OSMN là hình thoi;
- Các điểm P, Q, R lần lượt là các điểm đối xứng của các điểm S, M, N qua tâm O.
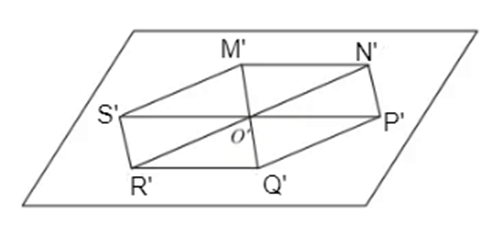
Từ đó suy ra các vẽ hình biểu diễn của hình lục giác đều MNPQRS như sau:
- Vẽ hình bình hành O'S'M'N' biểu diễn cho hình thoi OSMN;
- Lấy các điểm P', Q', R' lần lượt là các điểm đối xứng của các điểm S', M', N' qua O', ta được hình biểu diễn M'N'P'Q'R'S' của hình lục giác đều MNPQRS.
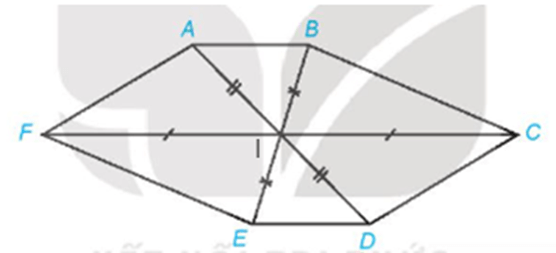
+) Gọi I là giao điểm các đường chéo AD, BE và CF trong hình lục giác ABCDEF ở Hình 4.65.
Khi đó nếu ABCDEF là hình biểu diễn của hình lục giác đều thì phải thỏa mãn hai điều kiện:
- Tứ giác IFAB là hình bình hành (1);
- D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua I (2).
Từ hình vẽ ta thấy điều kiện (2) thỏa mãn nhưng điều kiện (1) không thỏa mãn. Vậy Hình 4.65 không thể là hình biểu diễn của một hình lục giác đều.
Lời giải bài tập Toán 11 Bài 14: Phép chiếu song song hay, chi tiết khác:
Luyện tập 1 trang 97 Toán 11 Tập 1: Cho hình hộp ABCD.EFGH (H.4.58) ....
HĐ2 trang 97 Toán 11 Tập 1: Quan sát Hình 4.56a và trả lời các câu hỏi sau: ....