Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng a cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C sao cho \(\frac{{AB}}{{BC}} = \frac{2}{3}\) và đường thẳng b cắt
Câu hỏi:
Cho ba mặt phẳng (P), (Q), (R) đôi một song song với nhau. Đường thẳng a cắt các mặt phẳng (P), (Q), (R) lần lượt tại A, B, C sao cho \(\frac{{AB}}{{BC}} = \frac{2}{3}\) và đường thẳng b cắt các mặt phẳng (P), (Q), (R) lần lượt tại A', B', C'. Tỉ số \(\frac{{A'B'}}{{B'C'}}\) bằng
A. \(\frac{2}{3}\).
B. \(\frac{1}{2}\).
C. \(\frac{3}{2}\).
D. \(\frac{2}{5}\).
Trả lời:
Lời giải:
Đáp án đúng là: A
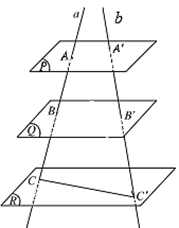
Theo định lí Thalés trong không gian, ta có \[\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}\].
Suy ra \(\frac{{A'B'}}{{B'C'}} = \frac{{AB}}{{BC}} = \frac{2}{3}\).
