Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, AA'. a) Xác định giao điểm của mặt phẳng (MNP) với đường thẳng B'C. b) Gọi K là giao điểm của
Câu hỏi:
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, AA'.
a) Xác định giao điểm của mặt phẳng (MNP) với đường thẳng B'C.
b) Gọi K là giao điểm của mặt phẳng (MNP) với đường thẳng B'C. Tính tỉ số \(\frac{{KB'}}{{KC}}\).
Trả lời:
Lời giải:
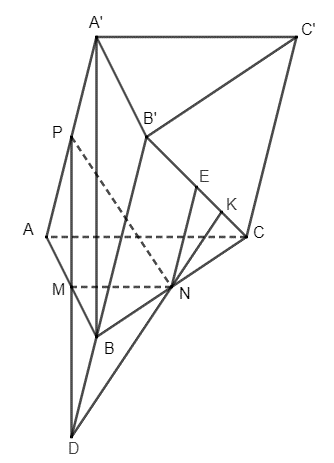
a) Trong mặt phẳng (ABB'A'), gọi D là giao điểm của PM và BB'.
Vì D thuộc BB' nên D thuộc mặt phẳng (BCC'B'), N thuộc BC nên N thuộc mặt phẳng (BCC'B'), do đó trong mặt phẳng (BCC'B') nối D với N, đường thẳng DN cắt B'C tại K.
Vì D thuộc PM nên D thuộc mặt phẳng (MNP), do đó DN nằm trong mặt phẳng (MNP).
Mà K thuộc DN nên K thuộc mặt phẳng (MNP).
Do vậy, K là giao điểm của mặt phẳng (MNP) với đường thẳng B'C.
b) Xét tam giác A'AB có P, M lần lượt là trung điểm của các cạnh AA', AB nên PM là đường trung bình của tam giác A'AB, suy ra PM // A'B hay PD // A'B.
Lại có A'P // BD (vì AA' // BB' do nó là các cạnh bên của hình lăng trụ tam giác ABC.A'B'C').
Do đó, tứ giác A'PDB là hình bình hành. Suy ra A'P = BD.
Mà P là trung điểm của AA' nên A'P = \(\frac{1}{2}\)AA', suy ra BD = \(\frac{1}{2}\)AA'.
Lại có AA' = BB' (do ABC.A'B'C' là hình lăng trụ tam giác).
Từ đó suy ra BD = \(\frac{1}{2}\)BB' (1) ⇒ \[\frac{{BD}}{{B'D}} = \frac{1}{3}\] (2).
Gọi E là trung điểm của B'C. Vì N là trung điểm của BC, do đó EN là đường trung bình của tam giác BB'C, suy ra EN // BB' và EN = \(\frac{1}{2}\)BB' (3).
Từ (1) và (3) suy ra EN = BD (4).
Từ (2) và (4) suy ra \[\frac{{EN}}{{B'D}} = \frac{1}{3}\].
Xét tam giác KDB' có EN // B'D (vì EN // BB'), theo định lí Thalés ta có:
\(\frac{{KE}}{{KB'}} = \frac{{EN}}{{B'D}} = \frac{1}{3}\).
Suy ra KE = \(\frac{1}{3}\)KB' ⇒ KE = \(\frac{1}{2}\)EB'.
Mà EB' = EC (do E là trung điểm của B'C).
Do đó, KE = \[\frac{1}{2}EC\]. Suy ra K là trung điểm của EC. Khi đó KC = \(\frac{1}{2}EC\).
Mà EC = \(\frac{1}{2}\)B'C. Suy ra KC = \[\frac{1}{2}.\frac{1}{2}B'C = \frac{1}{4}B'C\]. Từ đó suy ra KC = \(\frac{1}{3}\)KB'.
Vậy \(\frac{{KB'}}{{KC}} = 3\).
