Câu hỏi:
Trả lời:
Lời giải:
Ta có: \({u_n} - 3 = \frac{{{{3.2}^n} - 1}}{{{2^n}}} - 3 = \frac{{\left( {{{3.2}^n} - 1} \right) - {{3.2}^n}}}{{{2^n}}} = - \frac{1}{{{2^n}}} \to 0\) khi n ⟶ +∞.
Do vây, \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = 3\).
Câu 1:
Cho dãy số (un) với \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{n}\).
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ un đến 0 nhỏ hơn 0,01?
Câu 2:
Câu 3:
Cho dãy số (un) với \({u_n} = \frac{{n + {{\left( { - 1} \right)}^n}}}{n}\). Xét dãy số (vn) xác định bởi vn = un – 1.
Tính \(\mathop {\lim }\limits_{n \to + \infty } {v_n}\).
Câu 4:
Câu 5:
Cho hai dãy số (un) và (vn) với \({u_n} = 2 + \frac{1}{n},\,\,{v_n} = 3 - \frac{2}{n}\).
Tính và so sánh: \(\mathop {\lim }\limits_{n \to + \infty } \left( {{u_n} + {v_n}} \right)\) và \(\mathop {\lim }\limits_{n \to + \infty } {u_n} + \mathop {\lim }\limits_{n \to + \infty } {v_n}\).
Câu 6:
Câu 7:
Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau, sau đó tô màu hình vuông nhỏ góc dưới bên trái (H.5.2). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả sử quá trình trên tiếp diễn vô hạn lần. Gọi u1, u2, ..., un, ... lần lượt là độ dài cạnh của các hình vuông được tô màu.
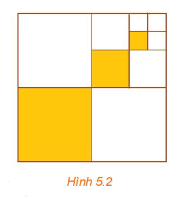
a) Tính tổng Sn = u1 + u2 + ... + un.
b) Tìm S = \(\mathop {\lim }\limits_{n \to + \infty } {S_n}\).
