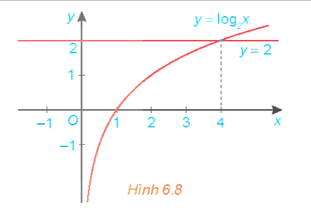
Cho đồ thị của các hàm số y = 2x và y = 4 như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số y = 2x nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình 2x > 4

Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô sau t năm sử dụng được mô hình hóa bằng công thức:

V(t) = 780 ∙ (0,905)^t.

Hỏi nếu theo mô hình này, sau bao nhiêu năm sử dụng thì giá trị của chiếc ô tô đó còn lại không quá 300 triệu đồng? (Làm tròn kết quả đến hàng đơn vị).

Xét phương trình:  $2^{x+1}=\frac{1}{4}$.

a) Khi viết  $\frac{1}{4}$ thành luỹ thừa của 2 thì phương trình trên trở thành phương trình nào?

b) So sánh số mũ của 2 ở hai vế của phương trình nhận được ở câu a để tìm x.

Giải các phương trình sau:

a)  $2^{3x-1}=\frac{1}{2^{x+1}}$;

Giải các bất phương trình sau:

a) 0,1^{2x – 1} ≤ 0,1^{2 – x};

Giải các bất phương trình sau:

b) 3 ∙ 2^{x + 1} ≤ 1.

Cho đồ thị của các hàm số y = log₂x và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số y = log₂x nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình log₂ x > 2.

Giải các bất phương trình sau:

a)  ${\log }_{\frac{1}{7}}\left(x+1\right)>{\log }_7\left(2-x\right)$;