Cho hình chóp S.ABC có SA (ABC). Gọi H là hình chiếu của A trên BC. a) Chứng minh rằng (SAB) (ABC) và (SAH) (SBC).
Câu hỏi:
Cho hình chóp S.ABC có SA ^ (ABC). Gọi H là hình chiếu của A trên BC.
a) Chứng minh rằng (SAB) ^ (ABC) và (SAH) ^ (SBC).
Trả lời:
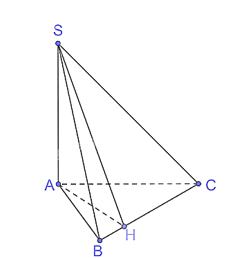
a) Vì SA ^ (ABC) nên (SAB) ^ (ABC).
Vì SA ^ (ABC) nên SA ^ BC.
Vì H là hình chiếu của A trên BC nên AH ^ BC.
Vì SA ^ BC và AH ^ BC nên BC ^ (SAH), suy ra (SAH) ^ (SBC).