Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.
Câu hỏi:
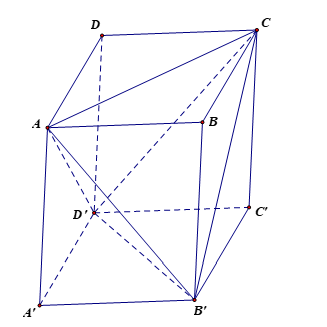
Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau. Chứng minh rằng tứ diện ACB'D' có các cặp cạnh đối diện vuông góc với nhau.
Trả lời:
Vì hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau nên các mặt của hình hộp là hình thoi.
Vì ABB'A' là hình thoi nên AB' ^ A'B.
Có CB // A'D' và CB = A'D' (do cùng song song và bằng AD). Do đó CBA'D' là hình bình hành, suy ra CD' // BA'.
Khi đó (CD', AB') = (BA', AB') = 90°.
Vậy CD' và AB' vuông góc với nhau.
Vì ADD'A' là hình thoi nên AD' ^ A'D.
Có CD // A'B' và CD = A'B' (vì CD, A'B' cùng song song và bằng AB) nên CDA'B' là hình bình hành, suy ra CB' // DA'.
Khi đó (CB', AD') = (DA', AD') = 90°.
Vậy CB' và AD' vuông góc với nhau.
Do ABCD là hình thoi nên AC ^ BD.
Vì BB' // DD' và BB' = DD' (do BB', DD' cùng song song và bằng AA' ) nên BDD'B' là hình bình hành, suy ra BD // B'D'.
Khi đó (AC, B'D') = (AC, BD) = 90°.
Vậy AC và B'D' vuông góc với nhau.