Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số h(t) = 90cos ( pi /10t), trong đó h(t) là độ cao tính bằng centimét trên mực nước
Câu hỏi:
Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số h(t) = \(90\cos \left( {\frac{\pi }{{10}}t} \right)\), trong đó h(t) là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm t giây.
a) Tìm chu kì của sóng.
b) Tìm chiều cao của sóng, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
Trả lời:
Lời giải:
a) Chu kì của sóng là \(T = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\) (giây).
b) Ta có: h(t) = \(90\cos \left( {\frac{\pi }{{10}}.t} \right)\), hàm số này có giá trị lớn nhất và nhỏ nhất lần lượt là 90 và – 90.
Vậy chiều cao của sóng là 180 cm.
Xem thêm lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết:
Câu 1:
Giả sử vận tốc v (tính bằng lít/giây) của luồng khí trong một chu kì hô hấp (tức là thời gian từ lúc bắt đầu của một nhịp thở đến khi bắt đầu của nhịp thở tiếp theo) của một người nào đó ở trạng thái nghỉ ngơi được cho bởi công thức
\(v = 0,85\sin \frac{{\pi t}}{3}\),
trong đó t là thời gian (tính bằng giây). Hãy tìm thời gian của một chu kì hô hấp đầy đủ và số chu kì hô hấp trong một phút của người đó.
Xem lời giải »
Câu 2:
Hoàn thành bảng sau:
|
x
|
sin x
|
cos x
|
tan x
|
cot x
|
|
\(\frac{\pi }{6}\)
|
?
|
?
|
?
|
?
|
|
0
|
?
|
?
|
?
|
?
|
|
\( - \frac{\pi }{2}\)
|
?
|
?
|
?
|
?
|
Xem lời giải »
Câu 3:
Tìm tập xác định của hàm số \(y = \frac{1}{{\sin x}}.\)
Xem lời giải »
Câu 4:
Cho hai hàm số f(x) = x2 và g(x) = x3, với các đồ thị như hình dưới đây.
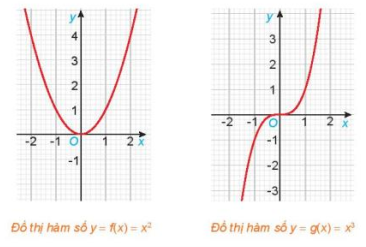
a) Tìm các tập xác định Df, Dg của các hàm số f(x) và g(x).
b) Chứng tỏ rằng f(– x) = f(x), ∀ x ∈ Df. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = f(x) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng g(– x) = – g(x), ∀ x ∈ Dg. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = g(x) đối với hệ trục tọa độ Oxy?
Xem lời giải »

