Câu hỏi:
Trả lời:
Lời giải:
Biểu thức \(\frac{1}{{\sin x}}\) có nghĩa khi sin x ≠ 0, tức là x ≠ kπ (k ∈ ℤ).
Vậy tập xác định của hàm số \(y = \frac{1}{{\sin x}}\) là ℝ \ {kπ | k ∈ ℤ}.
Câu 1:
Giả sử vận tốc v (tính bằng lít/giây) của luồng khí trong một chu kì hô hấp (tức là thời gian từ lúc bắt đầu của một nhịp thở đến khi bắt đầu của nhịp thở tiếp theo) của một người nào đó ở trạng thái nghỉ ngơi được cho bởi công thức
\(v = 0,85\sin \frac{{\pi t}}{3}\),
trong đó t là thời gian (tính bằng giây). Hãy tìm thời gian của một chu kì hô hấp đầy đủ và số chu kì hô hấp trong một phút của người đó.
Câu 2:
Hoàn thành bảng sau:
|
x |
sin x |
cos x |
tan x |
cot x |
|
\(\frac{\pi }{6}\) |
? |
? |
? |
? |
|
0 |
? |
? |
? |
? |
|
\( - \frac{\pi }{2}\) |
? |
? |
? |
? |
Câu 3:
Cho hai hàm số f(x) = x2 và g(x) = x3, với các đồ thị như hình dưới đây.
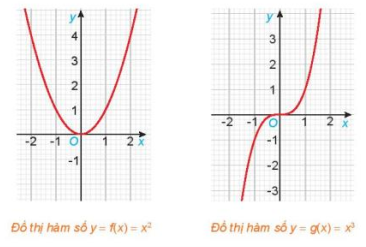
a) Tìm các tập xác định Df, Dg của các hàm số f(x) và g(x).
b) Chứng tỏ rằng f(– x) = f(x), ∀ x ∈ Df. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = f(x) đối với hệ trục tọa độ Oxy?
c) Chứng tỏ rằng g(– x) = – g(x), ∀ x ∈ Dg. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = g(x) đối với hệ trục tọa độ Oxy?
Câu 5:
So sánh:
a) sin(x + 2π) và sin x;
b) cos(x + 2π) và cos x;
c) tan(x + π) và tan x;
d) cot(x + π) và cot x.
Câu 6:
