HĐ4 trang 90 Toán 11 Tập 1 - Kết nối tri thức
Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46).
Giải Toán 11 Bài 13: Hai mặt phẳng song song - Kết nối tri thức
HĐ4 trang 90 Toán 11 Tập 1: Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46).
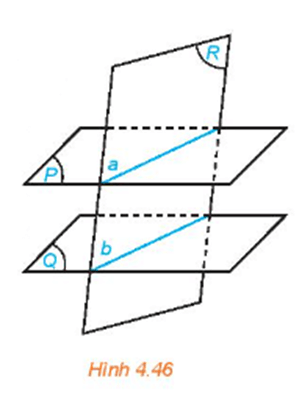
a) Giải thích vì sao mặt phẳng (R) cắt mặt phẳng (Q).
b) Gọi b là giao tuyến của hai mặt phẳng (R) và (Q). Hai đường thẳng a và b có thể chéo nhau hay không, có thể cắt nhau hay không?
Lời giải:
a) Giả sử mặt phẳng (R) không cắt mặt phẳng (Q), tức là hai mặt phẳng (R) và (Q) song song với nhau, mà mặt phẳng (P) song song với mặt phẳng (Q), do đó mặt phẳng (R) cũng song song với mặt phẳng (P) (hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau), mẫu thuẫn với giả thiết (R) cắt (P) theo giao tuyến a.
Vậy mặt phẳng (R) cắt mặt phẳng (Q).
b) Vì a và b cùng thuộc mặt phẳng (R) nên hai đường thẳng a và b không thể chéo nhau.
Hai đường thẳng a và b không có điểm chung, vì nếu chúng có điểm chung A thì hai mặt phẳng (P) và (Q) cũng có điểm chung A (mâu thuẫn với giả thiết (P) và (Q) song song với nhau). Vậy hai đường thẳng a và b không thể cắt nhau.
Lời giải bài tập Toán 11 Bài 13: Hai mặt phẳng song song hay, chi tiết khác:
Mở đầu trang 88 Toán 11 Tập 1: Các đầu bếp chuyên nghiệp luôn có kĩ năng dùng dao điêu luyện để thái thức ăn như rau, củ, thịt, cá ....
HĐ1 trang 88 Toán 11 Tập 1: Các mặt bậc thang trong Hình 4.40 gợi nên hình ảnh về các mặt phẳng không có điểm chung ....
Câu hỏi trang 88 Toán 11 Tập 1: Trong hình ảnh mở đầu, các nhát cắt có nằm trong các mặt phẳng song song hay không ....
HĐ2 trang 89 Toán 11 Tập 1: Cho mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β) ....
Câu hỏi trang 89 Toán 11 Tập 1: Nếu không có điều kiện “hai đường thẳng cắt nhau” thì khẳng định trên còn đúng không ....
Luyện tập 1 trang 89 Toán 11 Tập 1: Trong không gian, cho bốn điểm A, B, C, D không đồng phẳng ....
Vận dụng 1 trang 89 Toán 11 Tập 1: Một chiếc bàn có phần chân là hai khung sắt hình chữ nhật có thể xoay quanh một trục như trong Hình 4.43 ....
HĐ3 trang 89 Toán 11 Tập 1: Đặt một tấm bìa cứng lên một góc của mặt bàn nằm ngang (H.4.44) sao cho mặt bìa song song với mặt đất ....
Câu hỏi trang 89 Toán 11 Tập 1: Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì hai mặt phẳng đó có song song với nhau hay không ....
Luyện tập 2 trang 90 Toán 11 Tập 1: Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là các điểm thuộc cạnh SA, SB, SC, SD ....
Luyện tập 3 trang 91 Toán 11 Tập 1: Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD) ....
HĐ5 trang 91 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q) và (R) đôi một song song ....
Luyện tập 4 trang 91 Toán 11 Tập 1: Trong HĐ5, cho AB = 2 cm, BC = 4 cm và A'B' = 3 cm. ....
HĐ6 trang 91 Toán 11 Tập 1: Các hình ảnh dưới đây có đặc điểm chung nào với hình lăng trụ đứng tam giác mà em đã học ở lớp 7 ....
Câu hỏi trang 92 Toán 11 Tập 1: Hãy giải thích tại sao các mặt bên của hình lăng trụ là hình bình hành, từ đó suy ra các cạnh bên đôi một song song ....
Luyện tập 5 trang 92 Toán 11 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M và M' lần lượt là trung điểm của cạnh BC và B'C' ....
HĐ7 trang 92 Toán 11 Tập 1: Hình ảnh nào trong HĐ6 gợi nên hình ảnh về hình lăng trụ có đáy là hình bình hành? ....
Luyện tập 6 trang 93 Toán 11 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng hai mặt phẳng (ADD'A') và (BCC'B') song song với nhau ....

