Sử dụng định nghĩa, tính đạo hàm của các hàm số sau: b) y = x3.
Câu hỏi:
Sử dụng định nghĩa, tính đạo hàm của các hàm số sau:
b) y = x3.
Trả lời:
b) Đặt y = f(x) = x3.
Với x0 bất kì, ta có:
f'(x0) =
Vậy hàm số y = x3 có đạo hàm là hàm số y' = 3x2.
Câu hỏi:
Sử dụng định nghĩa, tính đạo hàm của các hàm số sau:
b) y = x3.
Trả lời:
b) Đặt y = f(x) = x3.
Với x0 bất kì, ta có:
f'(x0) =
Vậy hàm số y = x3 có đạo hàm là hàm số y' = 3x2.
Câu 1:
Nếu một quả bóng được thả rơi tự do từ đài quan sát trên sân thượng của tòa nhà Landmark 81 (Thành phố Hồ Chí Minh) cao 461,3 m xuống mặt đất. Có tính được vận tốc của quả bóng khi nó chạm đất hay không? (Bỏ qua sức cản không khí).
Câu 2:
Một vật di chuyển trên một đường thẳng (H.9.2). Quãng đường s của chuyển động là một hàm số của thời gian t, s = s(t) (được gọi là phương trình của chuyển động).
a) Tính vận tốc trung bình của vật trong khoảng thời gian từ t0 đến t.
Câu 4:
Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t, có dạng Q = Q(t).
a) Tính cường độ trung bình của dòng điện trong khoảng thời gian từ t0 đến t.
Câu 5:
Viết phương trình tiếp tuyến của parabol y = –x2 + 4x, biết:
a) Tiếp điểm có hoành độ x0 = 1;
Câu 6:
Viết phương trình tiếp tuyến của parabol y = –x2 + 4x, biết:
b) Tiếp điểm có tung độ y0 = 0.
Câu 7:
Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19,6 m/s thì độ cao h của nó (tính bằng mét) sau t giây được cho bởi công thức h = 19,6t – 4,9t2. Tìm vận tốc của vật khi nó chạm đất.
Câu 8:
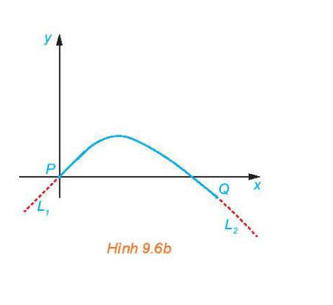
Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên L1 và đoạn dốc xuống L2 là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, L1 và L2 phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc tọa độ đặt tại P và phương trình của parabol là y = ax2 + bx + c, trong đó x tính bằng mét.
a) Tìm c.
b) Tính y'(0) và tìm b.