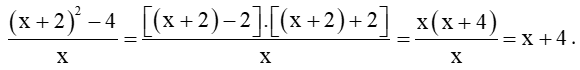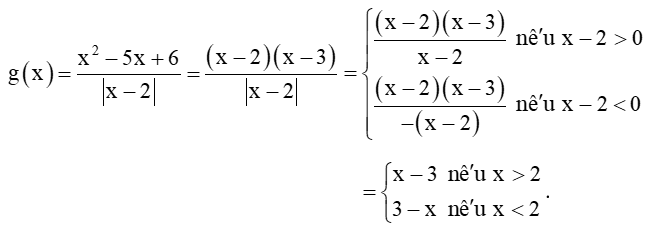Giải Toán 11 trang 118 Tập 1 Kết nối tri thức
Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 118 Tập 1 trong Bài 16: Giới hạn của hàm số Toán lớp 11 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 118.
Giải Toán 11 trang 118 Tập 1 Kết nối tri thức
Luyện tập 5 trang 118 Toán 11 Tập 1: Tính và .
Lời giải:
+) Ta có: , x – 2 > 0 với mọi x > 2 và
.
Do đó, .
+) Ta có: , x – 2 < 0 với mọi x < 2 và
.
Do đó, .
Bài 5.7 trang 118 Toán 11 Tập 1: Cho hai hàm số và g(x) = x + 1. Khẳng định nào sau đây là đúng?
a) f(x) = g(x);
b) .
Lời giải:
+) Biểu thức f(x) có nghĩa khi x – 1 ≠ 0 ⇔ x ≠ 1.
Ta có: , với mọi x ≠ 1.
Biểu thức g(x) = x + 1 có nghĩa với mọi x.
Do đó, điều kiện xác định của hai hàm số f(x) và g(x) khác nhau, vậy khẳng định a) là sai.
+) Ta có: ;
.
Vậy nên khẳng định b) là đúng.
Bài 5.8 trang 118 Toán 11 Tập 1: Tính các giới hạn sau:
a) ;
b) .
Lời giải:
Do mẫu thức có giới hạn là 0 khi x ⟶ 0 nên ta không thể áp dụng ngay quy tắc tính giới hạn của thương hai hàm số đối với cả hai câu a và b.
a) Ta có:
Do đó .
b) Ta có: .
Do đó .
Bài 5.9 trang 118 Toán 11 Tập 1: Cho hàm số 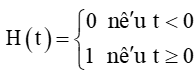
Tính và .
Lời giải:
Với dãy số (tn) bất kì sao cho tn < 0 và tn ⟶ 0, ta có H(tn) = 0.
Do đó .
Tương tự, với dãy số (tn) bất kì sao cho tn > 0 và tn ⟶ 0, ta có H(tn) = 1.
Do đó .
Bài 5.10 trang 118 Toán 11 Tập 1: Tính các giới hạn một bên:
a) ;
b) .
Lời giải:
a) Ta có: , x – 1 > 0 với mọi x > 1 và
.
Do đó, .
b) Ta có: , 4 – x > 0 với mọi x < 4 và
.
Do đó, .
Bài 5.11 trang 118 Toán 11 Tập 1: Cho hàm số 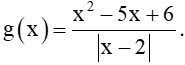
Tìm và .
Lời giải:
Ta có:
Do đó, ;
.
Bài 5.12 trang 118 Toán 11 Tập 1: Tính các giới hạn sau:
a) ;
b) .
Lời giải:
a) .
b) Ta có:
Do đó,
Bài 5.13 trang 118 Toán 11 Tập 1: Cho hàm số .
Tính và .
Lời giải:
Ta có:
+) và (do x – 2 > 0 khi x > 2).
Áp dụng quy tắc tìm giới hạn của tích, ta được .
+) và (do x – 2 < 0 khi x < 2).
Áp dụng quy tắc tìm giới hạn của tích, ta được .
Lời giải bài tập Toán 11 Bài 16: Giới hạn của hàm số Kết nối tri thức hay khác: